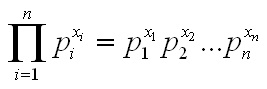|
|
||||||||||||||
| Links to Notebook Pages: | Mathematics |
Model Trains |
Friday August 4, 2006 5:45 am Lethbridge Alberta Sunrise 6:05 Sunset 9:09 Hours of daylight: 15:04
 |
 |
From rear window |
South patio |
Both images taken at noon. |
|
A. Morning Musings
5:45 am It is + 7 C at the moment, with a forecast high of + 26 C.
I have a cuppa beside me and am looking forward to continuing my Mathematics activity.
B. Plan
Immediate Health Walk & exercise 1 hr Mathematics Read "The Computational Beauty of Nature" Chap 3 3 hr Model Trains Wire lower mainline track for a power block 1 hr Assemble wooden trestle kit 1 hr Literature Begin reading "Ada Blackjack" 1 hr Later Chores Investigate water softeners for home 1 hr Technology Read manual for cell phone 1 hr add keywords to iPhoto records Make notes for chap. 4 of "Switching to the Mac" 2 hr Begin reading "iPhoto" 1 hr digital photography - learn about using the various manual settings Mathematics Larson "Calculus" Gardner "The Colossal Book of Short Puzzles" History Continue reading "Citizens" Watson "Ideas" Model Trains Add blue backdrop to layout 2 hr Assemble second oil platform kit
C. Actual/Notes
6:30 am
Now that I understand how to create mathematical notation in Windows and transfer the image to OS X, I am ready to continue my note making and reading of the third chapter of Gary Flake's book, "The Computational Beauty of Nature".
One strategy that I have when trying to Learn new material is to ask myself, 'what are the essential ideas of this section?' and 'Do I really understand this?'
What are the essential ideas of this section?
- It is possible to Godelize any number (or sequence of numbers, and hence any list). How does one do this?
First the idea. Godelizing a natural number (i.e. a positive integer) simply means creating a new natural number from the original number according to a well-defined procedure.
Second, why would one want to do this? The critical insight is realizing that it is possible to take any natural number and create a new natural number called the Godel number for the original number. Furthermore, the process is reversible. That is, given the Godel number one can determine the original number. And if it is possible to do this for any natural number, then it is also possible to do this for a (finite) string of such numbers. We already know that it is possible to think of a computer program as a sequence of integers. Thus every computer program has a corresponding Godel number. And given that number, we can determine the original program. This means that we can think about computer programs and determine some of their properties by considering the properties of the corresponding Godel numbers. Thus, much of computer science can be thought of in terms of the properties of integers. The converse is also true. One can think of the properties of integers in terms of computer programs.
It is also possible to think of numbers in terms of properties of functions such as continuity and differentiation. This is the heart of the Spivak book on calculus.
I wonder if thinking of integers in terms of programs might be a fruitful way to approach the Riemann hypothesis?
- "The key to the whole process is the fact that every number has a unique prime factorization. If you pick any natural number, x, then there is exactly one sequence of prime numbers,
such that the product of the n prime numbers is equal to x. Now let's go back to looking at a program's input, which we earlier agreed to think of as a sequence of numbers. If there are n numbers in the sequence, then let every number in the sequence be denoted by x1, x2, ... , xn. To calculate the Godel number of the input string, we use the first n prime numbers and calculate
which forms a unique natural number. Given a Godel number, we can reconstruct the original string by taking the prime factorization of the Godel number. If there are thirteen 2s in the prime factorization of the Godel number, then that means that the first number in the original string was 13. If there are eighty-seven 3s in the prime factorization, then the second number in the original string was 87." [p. 25]
8:30 am I have just had a skim of much of the book. This is truly an amazing book! I think that it will require a variety of approaches, some very slow and meticulous, others remaining at the skim level. But I think it would be a mistake to remain at either extreme for very long.
The book mentions that all the programs referred to in the book are available from a web site. Such programs are executable within a windows environment. I will try to obtain them now.
http://mitpress.mit.edu/flake/
Select Download Source Code from the menu on the left side.
Click on the cbn-mac-bin-sit.hqx to download a macintosh executable file which needs to be opened with Stuffit Expander. Save this file to the desktop.
The Mac file failed to open.
I then downloaded the windows file to the desktop and saved it in the windows partition on my external hard drive. I was able to open this zip file and then run the program stutter without difficulty. I think I am now set to use these programs while using Parallels to switch to the windows environment. 9:25 am
12:00 PM I am on day 2 of my electrician's apprenticeship. I have added a second barrier strip to the layout and have verified that my approach is still sound and not creating a short circuit. This took me about an hour. It takes time to to make sure that the wires are all cut to the proper length, to strip the ends of each piece of wire and to attach the wire to the terminal strip. I remember reading somewhere that one could use spade connectors instead of having to wrap the wire around the barrier screws. I would like to try this and see what I think of it in terms of ease and speed of installation.
Here is a photo of the first barrier strip that I installed yesterday with the additional wires leading out of it on the left that go to the second barrier strip.

The top two wires on the left attach to the terminal track section under the locomotive. The two bottom wires on the right go to the power source. I now have two barrier strips attached and have two more to go to complete the wiring for power for the Lower Mainline loop. This wiring will also work for when I convert over to DCC in a couple of months.
I added one additional turnout to the loop which will mean a revision to my diagram for the control panel. There is always some little adjustment that (hopefully) improves things a little.
D. Reflection