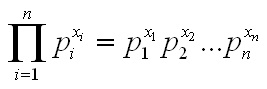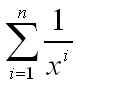|
|
|
Mathematics Chronology |
7:40 am
Chapter 3 on Computability and Incomputability has some very important, but very abstract, ideas. I recall reading about a strategy for Learning such material that was recommended by Richard Feynman. When one is no longer sure about what one is reading, go back to the beginning of the section and start over. It is a good strategy. A minor variation on this strategy is to also go back and make a new set of notes from the earlier notes.
It is worth remembering that I have all of the programs that are used in the book available for use within a Windows environment. This should encourage me to play with them when they are discussed in the book. |
3.1 Godelization
It is possible to think of a computer program as a sequence of integers. This entire sequence of integers can be used to compute a single Godel number. And given that number, we can determine the original program. This means that we can think about computer programs and determine some of their properties by considering the properties of the corresponding Godel numbers. Thus, much of computer science can be thought of in terms of the properties of integers. The converse is also true. One can think of the properties of integers in terms of computer programs.
- "The key to the whole process is the fact that every number has a unique prime factorization. If you pick any natural number, x, then there is exactly one sequence of prime numbers,
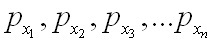
such that the product of the n prime numbers is equal to x. Now let's go back to looking at a program's input, which we earlier agreed to think of as a sequence of numbers. If there are n numbers in the sequence, then let every number in the sequence be denoted by x1, x2, ... , xn. To calculate the Godel number of the input string, we use the first n prime numbers and calculate
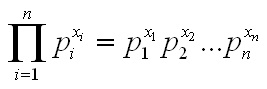
which forms a unique natural number. Given a Godel number, we can reconstruct the original string by taking the prime factorization of the Godel number. If there are thirteen 2s in the prime factorization of the Godel number, then that means that the first number in the original string was 13. If there are eighty-seven 3s in the prime factorization, then the second number in the original string was 87." [p. 25]
The essential idea underlying the Godel number is starting to make sense to me now. Once I have a Godel number it is relatively easy to find the prime factors of it. (either laboriously by trying each prime in order and keeping track of what still remains to be factored, or easily, by using a program like Mathematica).
On the other hand, this same principle is at the heart of much of the literature on cryptography. When the numbers become very very large, then the time taken to find the prime factors may be impractically long. I suspect that is what is meant by incomputability. I shall see. ... |
Since every program can be represented as a string of numbers, and since every string of numbers can be represented as a single Godel number, which is also a natural number (i.e. positive integer) then it follows that the number of possible programs is the same as the number of natural numbers (which is a form of infinity).
3.2 Models of Computation
- A computation is a "method" for producing one number from another. A "model of computation" is a description of how one might produce such a method. One such family of models are known as general recursive functions. For example, the Successor function adds one to its argument.
General recursive functions, Turing machines, and l-calculus are three well known models of computation. There are many others. Church proved, in 1941, that general recursive functions and l-calculus were equivalent. Turing later proved that Turing machines and l-calculus were equivalent, thus implying that all three models were equivalent.
Any function that can be computed by these models is called computable. Every model of computation that has been considered so far has been shown to be equivalent to (or weaker than) one of these three models.
3.3 Lisp and Stutter
I have realized that the different sections of the chapter provide an excellent way of compartmentalizing the topics in this chapter. I have gone back and added the section headings (in bold blue) to help make this structure explicit in my notes. Here are the remaining sections for this chapter:
3.4 Equivalence and Time Complexity
3.5 Universal Computation and Decision Problems
3.6 Incomputability
3.7 Number Sets Revisited
There are many genuinely new ideas in this chapter. It is worth proceeding slowly and carefully. |
Lisp is a computer language created in the 1950s by John McCarthy that is based on the ideas of l-calculus and general recursive functions. Lisp is still in common use today.
Stutter is a subset of Lisp. I have a working copy of Stutter in my Windows environment.
| At least for the moment I am going to ignore the details of the Stutter examples and move on to the next section. What is important for me at the moment is simply to realize that Stutter is a simple programming language that is capable of doing everything that the three models of computation are capable of. |
9:00 am
|
|
|
|
Mathematics Chronology |
6:30 am
Now that I understand how to create mathematical notation in Windows and transfer the image to OS X, I am ready to continue my note making and reading of the third chapter of Gary Flake's book, "The Computational Beauty of Nature".
One strategy that I have when trying to Learn new material is to ask myself, 'what are the essential ideas of this section?' and 'Do I really understand this?'
What are the essential ideas of this section?
- It is possible to Godelize any number (or sequence of numbers, and hence any list). How does one do this?
|
First the idea. Godelizing a natural number (i.e. a positive integer) simply means creating a new natural number from the original number according to a well-defined procedure.
Second, why would one want to do this? The critical insight is realizing that it is possible to take any natural number and create a new natural number called the Godel number for the original number. Furthermore, the process is reversible. That is, given the Godel number one can determine the original number. And if it is possible to do this for any natural number, then it is also possible to do this for a (finite) string of such numbers. We already know that it is possible to think of a computer program as a sequence of integers. Thus every computer program has a corresponding Godel number. And given that number, we can determine the original program. This means that we can think about computer programs and determine some of their properties by considering the properties of the corresponding Godel numbers. Thus, much of computer science can be thought of in terms of the properties of integers. The converse is also true. One can think of the properties of integers in terms of computer programs.
It is also possible to think of numbers in terms of properties of functions such as continuity and differentiation. This is the heart of the Spivak book on calculus.
I wonder if thinking of integers in terms of programs might be a fruitful way to approach the Riemann hypothesis? |
- "The key to the whole process is the fact that every number has a unique prime factorization. If you pick any natural number, x, then there is exactly one sequence of prime numbers,
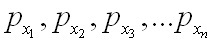
such that the product of the n prime numbers is equal to x. Now let's go back to looking at a program's input, which we earlier agreed to think of as a sequence of numbers. If there are n numbers in the sequence, then let every number in the sequence be denoted by x1, x2, ... , xn. To calculate the Godel number of the input string, we use the first n prime numbers and calculate
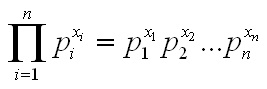
which forms a unique natural number. Given a Godel number, we can reconstruct the original string by taking the prime factorization of the Godel number. If there are thirteen 2s in the prime factorization of the Godel number, then that means that the first number in the original string was 13. If there are eighty-seven 3s in the prime factorization, then the second number in the original string was 87." [p. 25]
8:30 am I have just had a skim of much of the book. This is truly an amazing book! I think that it will require a variety of approaches, some very slow and meticulous, others remaining at the skim level. But I think it would be a mistake to remain at either extreme for very long.
The book mentions that all the programs referred to in the book are available from a web site. Such programs are executable within a windows environment. I will try to obtain them now.
http://mitpress.mit.edu/flake/
Select Download Source Code from the menu on the left side.
Click on the cbn-mac-bin-sit.hqx to download a macintosh executable file which needs to be opened with Stuffit Expander. Save this file to the desktop.
The Mac file failed to open.
I then downloaded the windows file to the desktop and saved it in the windows partition on my external hard drive. I was able to open this zip file and then run the program stutter without difficulty. I think I am now set to use these programs while using Parallels to switch to the windows environment. 9:25 am |
|
|
|
|
Mathematics Chronology |
6:00 am My previous attempt to begin Gary Flake's book, "The Computational Beauty of Nature" was on June 22. I have reread these and am now about to begin reading chapter 3 Computability and Incomputability. [pp. 23 - 49]
- "Computer Science is no more about computers than astronomy is about telescopes. - E. W. Dijkstra" [p. 23]
- "If we could not reduce what happens inside of computers into some mathematical formalism, there would be no way of proving or disproving the properties that computers have." [p. 24]
- "... it is possible (and also theoretically useful) to convert a program, input string, or output string into a single natural number." [p. 24]
| This is a great sentence. It it crystal clear and yet mind-boggling at the same time. |
- "A Godelization is a method for mapping many natural numbers into a single natural number." [p. 25]
| This is a new term for me, and also a new idea. I am not sure what to do with it yet, but I sense that it is a very powerful idea as it appears to be an ultimate form of condensation. |
- "... we will sometimes refer to the computation as manipulating strings, numbers, or even bits. It really doesn't matter. What does matter is that the representation of a computer's input and output can always be converted from one form to another. We will simply use whatever form is most convenient at the time." [p. 26]
- "Another conclusion that can be reached from the ideas in this section is that there are as many programs as there are natural numbers." [p. 26]
| I love the way Flake extends the ideas in a very natural way to conclusions that are staggering in their novelty. |
Whoa! Time to slow down. One strategy that I have when trying to Learn new material is to ask myself, 'what are the essential ideas of this section?' and 'Do I really understand this?'
What are the essential ideas of this section?
- It is possible to Godelize any number (or sequence of numbers, and hence any list). How does one do this?
- Pick any natural number x. This number has a unique prime factorization
Whoa again! I want to continue making my notes using mathematical notation that exceeds the capabilities of Dreamweaver. In a Windows environment I have used a program called MathType that allowed me to use Word to easily create such mathematical expressions and then copy them as a gif file into Dreamweaver. A quick google search shows that there is a version of MathType for the Mac, but it costs about $150. I wonder if I can use Parallels software on the Mac to switch to Windows and then copy the expression and switch back to OS X and paste it into this page.
Whoa, whoa again. I seem to have a problem booting up Parallels. I suspect that it is related to something I did a couple of weeks ago when I changed some form of Home setting. I will contact the uni later this morning and see if they have any suggestions.
Okay, a quick phone call solved the problem of Parallels. The next test was to see if it would allow a copy&paste across operating systems. The answer to this appears to be no. I tried it copying selected text as well as an image, but in both cases when I switched to OS X there was nothing to paste. It looks like I will need to order MathType for the Mac.
Success! The trick is to form the appropriate expression using MathType in Windows, then use Parallels to switch back to OS X, then use Grab to select the area of the Windows display that I want , save this as a TIFF to the desktop, then select it and save it as a JPEG file. Finally select the image in the Dreamweaver website and it will ask if I want it saved in the website and then display it as with any image. Simple when you know how.
The above is a sample screen capture from a windows display.
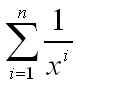
What started out as a Mathematics activity quickly became a Technology activity. But a satisfying one as I am now becoming comfortable with both Parallels and MathType in Windows. Actually this is quite cool. |
|
|