index.html

Saturday, May 9 2009
9:10 am
I will stay with the Stylesheet "Classroom"

Chapter 1 Getting Started
1.8 Using Variables
Variables are defined by means of the equal symbol.

In[1]:=

Out[1]=

Out[2]=

Out[3]=

One of the real powers of Mathematica is that it can manipulate abstract expressions. This is sometimes called symbolic computation.
Here is an example using the function Expand:

In[4]:=

Out[4]=

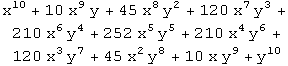
x^10 + 10 x^9 y + 45 x^8 y^2 + 120 x^7 y^3 + 210 x^6 y^4 + 252 x^5 y^5 + 210 x^4 y^6 + 120 x^3 y^7 + 45 x^2 y^8 + 10 x y^9 + y^10

I would not want to do this by hand.
1.9 Using Comments
This section is not as useful as simply using alt-7 to change to Text (as I am doing at the moment).

1.10 Suppressing Output
Sometimes the result of a calculation can produce a large amount of output.

In[6]:=

Out[6]=

13220708194808066368904552597521443659654220327521481676649203682268285973467048995407783138 ... 695516765018940588109060426089671438864102814350385648747165832010614366132173102768902855220001

This output can be suppressed by adding a ; to the end of the expression.

In[10]:=

In[12]:=

In[13]:=

Out[13]=

13220708194808066368904552597521443659654220327521481676649203682268285973467048995407783138 ... 695516765018940588109060426089671438864102814350385648747165832010614366132173102768902855220002

There is a Quiz at the end of the chapter.
1. Use Mathematica to compute exactly.

In[14]:=

Out[14]=

2. Use Mathematica to compute and represent the answer in decimal form.

In[15]:=

Out[15]=

3. It turns out tha the numbers and are pretty close to each other. Without computing them it is not easy to see which is bigger. Use Mathematica to find out which number is bigger.

In[16]:=

Out[16]=

I can verify this by computing each number to a certain number of decimal places.

In[17]:=

Out[17]=

In[18]:=

Out[18]=

4. The volume of a ball of radius r is given by V = π and its surface area is given by A = 4π. The radius of the earth is about 4000 miles. Use Mathematica to estimate the volume and surfce area of the earth.

In[23]:=

In[24]:=

Out[24]=

In[29]:=

Out[29]=

In[30]:=

Out[30]=

In[32]:=

Out[32]=

This last problem was excellent as it reminded me to leave a space between each symbol for implied multiplication.

In[35]:=

In[36]:=

Out[36]=

In[37]:=

Out[37]=

5. The volume of any cone is one-third the area of the base times the height, where the height is measured perpendicular to the base. The Great Pyramid at Cheops has a square base about 230 meters on a side and its height is about 147 meters high. Use Mathematica to compute the volume of the pyramid.

In[39]:=

Out[39]=

Out[40]=

Out[41]=

6. Use the Table function to make a list of the cubes of the first 10 integers.

In[43]:=

$cubes = Table[x^3, {x, 1, 10}]$

Out[43]=

In[44]:=

Out[44]=

7. The sine function is given by Sin. Use the Table function to make a table of sin x for every x from 0 to π/2 in increments of π/20. Have the entries in the table in decimal form.

In[45]:=

Out[45]=

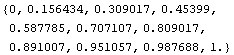
{0, 0.156434, 0.309017, 0.45399, 0.587785, 0.707107, 0.809017, 0.891007, 0.951057, 0.987688, 1.}

This is one way of obtaining values of a trigonometric function. But usually I will want to see the corresponding graph.
8. The number e is defined as the limit of as n approaches infinity. Use the Table function to list the value of for n = 10, , , ... .

In[46]:=

$Table[(1. + 1/10^k)^10^k, {k, 1, 6}]$

Out[46]=

9. The function n! which is read as "n factorial" is defined to be the product of all positive integers from 1 to n. Use the Table function to make a list of n! for n = 1 to 20.

In[48]:=

Out[48]=

{1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, 87178 ... 000, 20922789888000, 355687428096000, 6402373705728000, 121645100408832000, 2432902008176640000}

In[49]:=

Out[49]=

A good morning session. I am making good use of the Basic Math Input Palette.
11:00 am

Created by Mathematica (May 9, 2009)