|
||||||||||
Wednesday January 24, 2007 6:05 am Lethbridge Sunrise 8:15 Sunset 17:12 Hours of daylight: 8:57
A. Morning Musings
6:05 am It is +10 C at the moment with a high of +13 C forecast - still windy: 48 km/h with gusts to 59 km/h.
Here are the news.
CBC Headline: Iraq, Healthcare, Energy Top Bush's State of the Union Address
US politics. All talk.
Canadian Headline: Videotaped Evidence to Continue at Pickton Trial
This is still our main headline. The videotapes are of an interview between Pickton and a police officer before he was charged with the murders.
Australian Headline: (from The Australian): Inflation Figures Good News for Homeowners - PM
Federal politics. Inflation is at 3.3%, down from 3.9% a year ago. This should mean that there will not be a rise in interest rates in the near future.
My comments on the news have taken a nosedive. I do not view this as cynicism, but rationality.
I am hoping to receive a reply to an email I sent to Delicious Library. If the problem I had trying to import a tab-delimited file is simply that the option is turned off with the demo version, I will buy it.
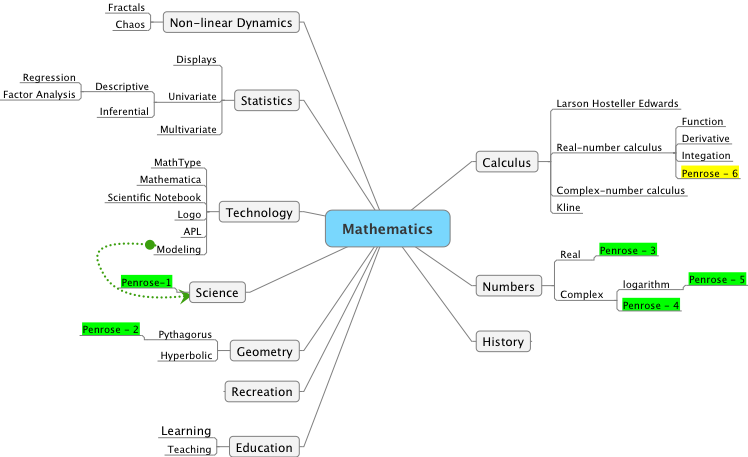
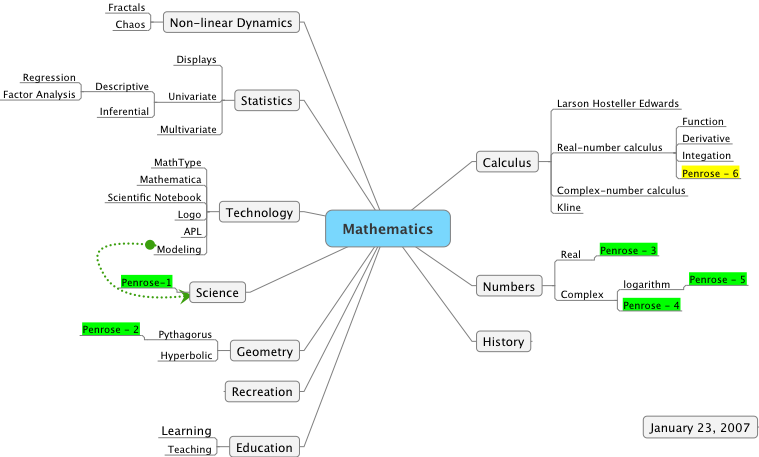
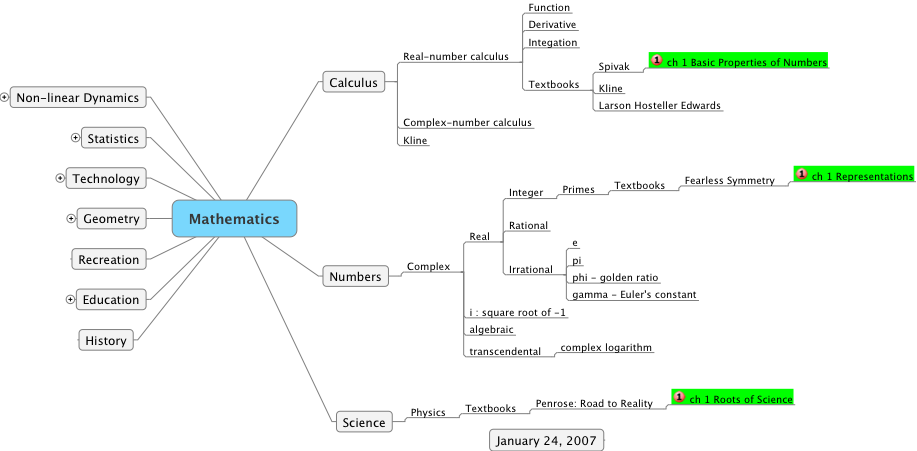
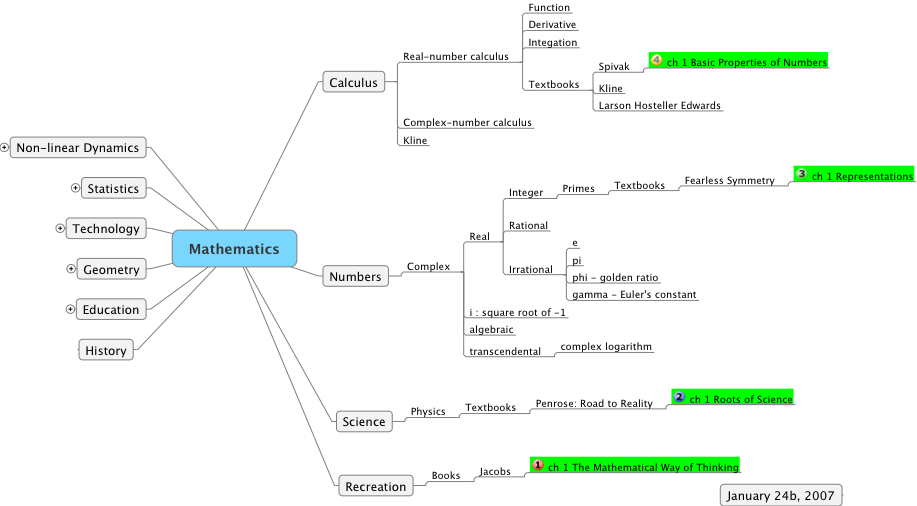
I also want to begin exploring the idea of a mind map for my mathematics.
B. Plan
Immediate Health Walk & exercise 1 hr Technology Begin reading "iPhoto" 1 hr Digital photography - learn about using the various manual settings 1 hr Preview Delicious Library software 1 hr Model Trains Follow tutorial for 3rdPlanIt (Manual p. 8 - 13) 1 hr Literature Complete reading "The Heart is an Involuntary Muscle" by Monique Proulx 1 hr Mathematics Create concept maps for my Learning of mathematics 2 hr Later Chores Investigate water softeners for home Technology Read manual for cell phone Make notes for chap. 4 of "Switching to the Mac" Burn backup of images onto DVD Edit iPhoto images Mathematics Read "Fearless Symmetry" chap 9: Elliptic Curves Model Trains Add ground cover to oil refinery diorama Continue assembly of coaling tower Purchase DCC system History Read Watson "Ideas" Philosophy Read & make notes for "Breaking the Spell" GO Complete reading "Lessons in the Fundamentals of Go" Puzzles The Orange Puzzle Cube: puzzle #10
C. Actual/Note
 |
|||||
|
|||||
D. Reflection
9:40 PM A satisfying day. The early morning math session was a delight.
Later this morning I was finally able to buy some cement for bonding my plastic models together. This means I can now continue to work on these models for my model train layout.
Then I received an email from the folk at Delicious Library indicating that I needed to add a header record to my tab-delimited file in order to import records from a database. Done. I then thoroughly explored the features and was quite impressed with the capabilities of the package. It is tempting to order it , but when I sit back and ask myself whether I would really gain value from it, I find the answer to be no. I am quite familiar with most of my books and do not need a search engine to find my way through them.
I then spent a very enjoyable hour in the afternoon finishing "The Heart is an Involuntary Muscle" by Monique Proulx. I will try to make a few notes in the next day or two.