August 20, 2007
This session is based on the material in section 3.1 of Kelley's "The Humongous Book of Calculus Problems"
The section presents a series of problems involving adding and subtracting rational polynomials.
Problem 3.1

Clear All

All Clear

fn1 = 5/y

5/y

fn2 = -3/x^2

-3/x^2

fn3 = fn1 + fn2

-3/x^2 + 5/y

fn4 = Together[fn1 + fn2]

(5 x^2 - 3 y)/(x^2 y)

p1 = Plot[fn1, {y, -10, 10}, PlotStyleRed] ;

[Graphics:HTMLFiles/index_12.gif]

p2 = Plot[fn2, {x, -10, 10}, PlotStyleBlue] ;

[Graphics:HTMLFiles/index_14.gif]

Show[p1, p2] ;

[Graphics:HTMLFiles/index_16.gif]

The next step is not clear to me.
I want a graph of fn4, but am not sure how to obtain it.
Let's try ImplicitPlot.

<<Graphics`ImplicitPlot`

p3 = ImplicitPlot[fn40, {x, -1, 1}] ;

1 Power :: infy : Infinite expression ---- encountered. More… 2 0.`

[Graphics:HTMLFiles/index_20.gif]

Show[p1, p2, p3] ;

... x y

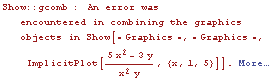
Let's try a straight forward approach.

Plot[fn1 + fn2, {x, -10, 10}] ;

Plot :: plnr : fn1 + fn2 is not a machine-size real number at x = -9.999999166666667`. More…

Plot :: plnr : fn1 + fn2 is not a machine-size real number at x = -9.188660168541684`. More…

Plot :: plnr : fn1 + fn2 is not a machine-size real number at x = -8.303824002812526`. More…

General :: stop : Further output of Plot :: plnr will be suppressed during this calculation. More…

[Graphics:HTMLFiles/index_28.gif]

fn1 + fn2

-3/x^2 + 5/y

Let's try Parametric Plot.

ft1 = 5/t

5/t

ft2 = -3/t^2

-3/t^2

ft1 + ft2

-3/t^2 + 5/t

p3 = Plot[ft1 + ft2, {t, -10, 10}] ;

[Graphics:HTMLFiles/index_38.gif]

This look like it!

Show[p1, p2, p3] ;

[Graphics:HTMLFiles/index_40.gif]

Clear All

All Clear

fn1 = (x^2)/(18y)

x^2/(18 y)

fn2 = (7y)/(3z)

(7 y)/(3 z)

fn3 = (5z^3)/(12x)

(5 z^3)/(12 x)

fn4 = Together[fn1 - fn2 + fn3]

(-84 x y^2 + 2 x^3 z + 15 y z^4)/(36 x y z)

Plot3D[fn1, {x, -10, 10}, {y, -10, 10}] ;

[Graphics:HTMLFiles/index_52.gif]

Plot3D[fn2, {y, -10, 10}, {z, -10, 10}] ;

[Graphics:HTMLFiles/index_54.gif]

Plot3D[fn3, {x, -10, 10}, {z, -10, 10}] ;

[Graphics:HTMLFiles/index_56.gif]

Plot3D[fn4, {x, -10, 10}, {y, -10, 10}] ;

Plot3D :: plnc : fn4 is neither a machine-size real number at {x, y} = {-10.`, -10.`} nor a list of a real number and a valid color directive. More…

Plot3D :: plnc : fn4 is neither a machine-size real number at {x, y} = {-9.166666666666666`, -10.`} nor a list of a real number and a valid color directive. More…

Plot3D :: plnc : fn4 is neither a machine-size real number at {x, y} = {-8.333333333333332`, -10.`} nor a list of a real number and a valid color directive. More…

General :: stop : Further output of Plot3D :: plnc will be suppressed during this calculation. More…

... not a real number. More… z

... real number. More… z

0.00033333333333333343` (1) Plot3D :: gval ... yi = 3 is not a real number. More… z

General :: stop : Further output of Plot3D :: gval will be suppressed during this calculation. More…

[Graphics:HTMLFiles/index_66.gif]

Once again, I am not sure how to proceed. My difficulty lies with my weak understanding of what a parametric plot (or an implicit plot) really is.

August 21, 2007
This will be my second attempt to obtain a parametric plot in 3D for this situation.

In[1]:=

Clear All

Out[1]=

All Clear

In[2]:=

<<Graphics`ParametricPlot3D`

In[7]:=

fxy = (x^2)/(18y)

Out[7]=

x^2/(18 y)

In[8]:=

Plot3D[fxy, {x, -10, 10}, {y, -10, 10}] ;

[Graphics:HTMLFiles/index_73.gif]

In[9]:=

ParametricPlot3D[{x, y, fxy}, {x, -10, 10}, {y, -10, 10}] ;

[Graphics:HTMLFiles/index_75.gif]

In[10]:=

fxt = (x^2)/(18t)

Out[10]=

x^2/(18 t)

In[11]:=

fyt = (7y)/(3t)

Out[11]=

(7 y)/(3 t)

In[12]:=

fzt = (5z^3)/(12t)

Out[12]=

(5 z^3)/(12 t)

In[13]:=

f = fxt - fyt + fzt

Out[13]=

x^2/(18 t) - (7 y)/(3 t) + (5 z^3)/(12 t)

In[15]:=

ParametricPlot3D[{fxt, x, t}, {x, -10, 10}, {t, -10, 10}] ;

[Graphics:HTMLFiles/index_85.gif]

In[16]:=

ParametricPlot3D[{fyt, y, t}, {y, -10, 10}, {t, -10, 10}] ;

[Graphics:HTMLFiles/index_87.gif]

In[17]:=

ParametricPlot3D[{fzt, z, t}, {z, -10, 10}, {t, -10, 10}] ;

[Graphics:HTMLFiles/index_89.gif]

In[19]:=

ParametricPlot3D[{f, x, y, z, t}, {x, -10, 10}, {y, -10, 10}, {z, -10, 10}] ;

ParametricPlot3D :: nonopt : Options expected (instead of {z, -10, 10}) beyond position 3 i ... 10, 10}, {y, -10, 10}, {z, -10, 10}] . An option must be a rule or a list of rules. More…

Nope. I still don't get it.
Let's try moving back to two dimensions.

In[20]:=

fx = t^2

Out[20]=

t^2

In[21]:=

fy = 4t^2

Out[21]=

4 t^2

In[24]:=

ParametricPlot[{fx, fy}, {t, -10, 10}] ;

[Graphics:HTMLFiles/index_97.gif]

This "feels" a little better, but I am still not grasping the idea.

I am going to see what happens if I follow the logic of the first problem for this situation.

In[25]:=

Clear All

Out[25]=

All Clear

In[27]:=

fxy = (x^2)/(18y)

Out[27]=

x^2/(18 y)

In[28]:=

fyz = (7y)/(3z)

Out[28]=

(7 y)/(3 z)

In[29]:=

fxz = (5z^3)/(12x)

Out[29]=

(5 z^3)/(12 x)

In[30]:=

Plot3D[fxy, {x, -10, 10}, {y, -10, 10}] ;

[Graphics:HTMLFiles/index_107.gif]

In[31]:=

fsum = fxy - fyz + fxz

Out[31]=

x^2/(18 y) - (7 y)/(3 z) + (5 z^3)/(12 x)

In[33]:=

fsum2 = Together[fxy - fyz + fxz]

Out[33]=

(-84 x y^2 + 2 x^3 z + 15 y z^4)/(36 x y z)

In[34]:=

fxt = t/18

Out[34]=

t/18

In[35]:=

fyt = 7/3

Out[35]=

7/3

In[36]:=

fzt = (5t^2)/12

Out[36]=

(5 t^2)/12

In[41]:=

p1 = Plot[fxt, {t, -10, 10}, PlotStyleRed] ;

[Graphics:HTMLFiles/index_119.gif]

In[42]:=

p2 = Plot[fyt, {t, -10, 10}, PlotStyleBlue] ;

[Graphics:HTMLFiles/index_121.gif]

In[43]:=

p3 = Plot[fzt, {t, -10, 10}, PlotStyleGreen] ;

[Graphics:HTMLFiles/index_123.gif]

In[45]:=

Show[{p1, p2, p3}] ;

[Graphics:HTMLFiles/index_125.gif]

In[49]:=

fsum = fxt - fyt + fzt

Out[49]=

-7/3 + t/18 + (5 t^2)/12

In[50]:=

p4 = Plot[fsum, {t, -10, 10}] ;

[Graphics:HTMLFiles/index_129.gif]

In[51]:=

Show[{p1, p2, p3, p4}] ;

[Graphics:HTMLFiles/index_131.gif]

Finally. This seems to make sense. The black line is the arithmetic combination of the three colored lines.

#3.4

In[68]:=

f1 = (w + 1)/(14w^4)

Out[68]=

(1 + w)/(14 w^4)

In[69]:=

f2 = 5/((w^3) - 3w^2)

Out[69]=

5/(-3 w^2 + w^3)

In[70]:=

f3 = f1 - f2

Out[70]=

(1 + w)/(14 w^4) - 5/(-3 w^2 + w^3)

In[71]:=

f3 = Together[f1 - f2]

Out[71]=

(-3 - 2 w - 69 w^2)/(14 (-3 + w) w^4)

In[73]:=

p1 = Plot[f1, {w, -10, 10}, PlotStyleRed] ;

[Graphics:HTMLFiles/index_141.gif]

In[74]:=

p2 = Plot[f2, {w, -10, 10}, PlotStyleBlue] ;

[Graphics:HTMLFiles/index_143.gif]

In[75]:=

Show[p1, p2] ;

[Graphics:HTMLFiles/index_145.gif]

In[76]:=

p3 = Plot[f3, {w, -10, 10}] ;

[Graphics:HTMLFiles/index_147.gif]

In[77]:=

Show[p1, p2, p3] ;

From In[77]:=

[Graphics:HTMLFiles/index_149.gif]

This seems okay.

In[78]:=

Clear All

Out[78]=

All Clear

In[79]:=

f1 = (x - 2)/(5x^2 - 45)

Out[79]=

(-2 + x)/(-45 + 5 x^2)

In[80]:=

f2 = (2x - 3)/(x^2 - x - 12)

Out[80]=

(-3 + 2 x)/(-12 - x + x^2)

In[81]:=

f3 = f1 - f2

Out[81]=

-(-3 + 2 x)/(-12 - x + x^2) + (-2 + x)/(-45 + 5 x^2)

In[82]:=

p1 = Plot[f1, {x, -10, 10}, PlotStyleRed] ;

[Graphics:HTMLFiles/index_159.gif]

In[83]:=

p2 = Plot[f2, {x, -10, 10}, PlotStyleBlue] ;

[Graphics:HTMLFiles/index_161.gif]

In[84]:=

p3 = Plot[f3, {x, -10, 10}] ;

[Graphics:HTMLFiles/index_163.gif]

In[85]:=

Show[p1, p2, p3] ;

[Graphics:HTMLFiles/index_165.gif]

Created by Mathematica  (August 21, 2007) Valid XHTML 1.1!