Session 7 (week 4a)

Chapter 2 Polynomials

Section 2.3 Factoring Polynomials

1. Activities

W. Michael Kelley (2006). The Humongous Book of Calculus Problems.

Complete problems 2.20 - 2.27 [p. 21 - 23]

Wayne W. Dyer (2007). Change Your Thoughts - Change Your Life.

Read Verse 7: Living Beyond Ego [p. 33 - 38]

2. What's it all about?

This is preparation for the next section on solving quadratic equations.

3. What am I able to do, now that I am finished this section?

• find common factors in a series of polynomial terms
• find the two integral factors in a quadratic polynomial
• find the two factors in a cubic polynomial
• find the two factors in the polynomial x^3 + y^3
• find the two factors in the polynomial x^3 - y^3

4. What will I know?

• I will become more proficient at noticing patterns in the coefficients of a polynomial

5. What are the key concepts?

• realizing that a polynomial can often be decomposed into a product of much simpler expressions

6. What are some relevant Web sites for this material?

Using your favorite search engine, and maybe one or two others, type in a few key words such as "polynomial factor".

Here are a few Web sites that I liked:

• http://www.sosmath.com/algebra/factor/fac02/fac02.html
• http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut7_factor.htm#gcf
• http://mathforum.org/dr.math/faq/faq.learn.factor.html
• http://faculty.ed.umuc.edu/~swalsh/Math%20Articles/Factoring.html

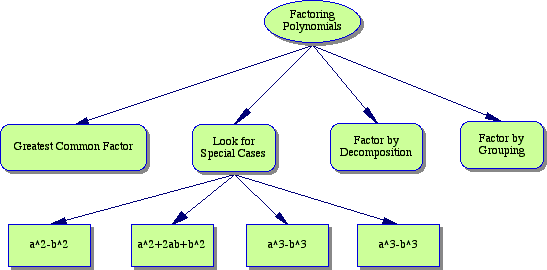
7. What concept map can I create for this section?

8. What types of Mathematica activities can I create?

Mathematica can find the factors of any polynomial with integral coefficients.

But there appears to be little value in doing this unless it is an important first step in some much longer problem. Just getting an answer is not the point. The point is to be able to understand why the answer is in fact correct. Another point is to become facile at noting patterns among various combinations.

9. What are some connections to other ideas?

This shows the close inter-relationship between the five basic algebraic operations. It is also important to realize that this is an important first step in finding the solutions to many quadratic and cubic polynomials.

10. What is my overall reaction to this section?

I have always enjoyed factoring polynomial expressions. I think it is because I am looking for patterns of numbers and variables that simplify a complex expression involving addition and subtraction of a large number of terms into a product of much simpler expressions.

11. Comments on Dyer: 7. Living Beyond Ego

The central idea of the 7th verse is to "serve the needs of others, and all your own needs will be satisfied". Mathematics, because it is a tight logical system, grows through the efforts of everyone who tries to extend it. Thus by trying to extend the boundaries of what is known one is preparing the way for those who may use this knowledge in the future.

By truly understanding the ideas of a mathematical topic one is also in a strong position to help others who are still trying to understand the concept. One is also in a better position to see how a particular mathematical idea may lead to the solution of a real-world problem. It also helps guard against arguments that involve a fallacious use of mathematics (particularly statistics).