Session 3 (week 2a)

Chapter 1 Linear Equations and Inequalities

Section 1.3 Absolute Value Equations and Inequalities

1. Activities

W. Michael Kelley (2006). The Humongous Book of Calculus Problems.

Complete problems 1.21 - 1.27 [p. 8 - 10]

Wayne W. Dyer (2007). Change Your Thoughts - Change Your Life.

Read Verse 3: Living Contentment [p. 13 - 18]

2. What's it all about?

This section describes solving equations and inequalities that involve the absolute value of an expression involving one unknown variable.

3. What am I able to do, now that I am finished this section?

I will be able to solve equations involving the absolute value of an expression involving one unknown.

I will be able to express the solution to an inequality involving an expression involving one unknown either algebraically, using interval notation and graphically.

4. What will I know?

I will understand the nature of the absolute value of an expression involving one unknown.

I will have a clear image of the geometric interpretation of an inequality involving an absolute value.

5. What are the key concepts?

• absolute value

6. What are some relevant Web sites for this material?

Using your favorite search engine, and maybe one or two others, type in a few key words such as "absolute value equations " or "absolute value inequalities".

Here are six Web sites that I liked:

• http://www.purplemath.com/modules/solveabs.htm
• http://www.analyzemath.com/Absolute_Value_Function/Absolute_Value_Function.html
• http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut21_abseq.htm
• http://www.purplemath.com/modules/absineq.htm
• http://www.sosmath.com/algebra/inequalities/ineq03/ineq03.html
• http://regentsprep.org/REgents/mathb/7D8/absinequal.htm

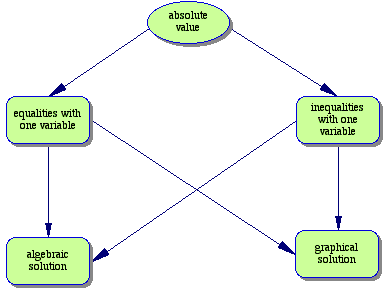
7. What concept map can I create for this section?

8. What types of Mathematica activities can I create?

This is useful if one is trying to learn more about some of the defined functions of Mathematica. It is also worthwhile if one is trying to see how one can use the absolute value function to obtain a graphical representation of a complex inequality.

9. What are some connections to other ideas?

The idea of interpreting the absolute value of an expression as a measure of the distance is useful.

10. What is my overall reaction to this section?

One must be very careful and meticulous when approaching this type of problem. It is very easy to forget the importance of both positive and negative values.

11. Comments on Dyer: 3. Living Contentment

Dyer suggests that the third verse of the Tao Te Ching implies that one should "bring happiness to every encounter in life". Try this advice when approaching any mathematics problem. Start off with the assumption that each problem is an opportunity to think, and that thinking is itself is an enjoyable activity. If the problem still leaves you confused, view this as an opportunity to learn something new. Once again, this is a positive event that allows you to grow. Fantastic. Every day is full of such opportunities.