Session 2 (week 1b)

Chapter 1 Linear Equations and Inequalities

Section 1.2 Linear Inequalities and Interval Notation

1. Activities

W. Michael Kelley (2006). The Humongous Book of Calculus Problems.

Complete problems 1.11 - 1.20 [p. 5 - 8]

Wayne W. Dyer (2007). Change Your Thoughts - Change Your Life.

Read Verse 2: Living the Paradoxical Mystery [p. 7 - 12]

2. What's it all about?

This section extends the idea of equality to inequalities and describes how to graph an inequality on the number line as well as how to write an inequality using a notational convention involving parentheses and brackets.

3. What am I able to do, now that I am finished this section?

Given an inequality equation, I can represent it on a number line and I can represent it symbolically.

4. What will I know?

I understand the basic idea of an inequality and that it can be represented both graphically and symbolically.

5. What are the key concepts?

• interval notation using parentheses and brackets
• graphical representation of an inequality involving one variable
• graphical representation of an inequality involving two variables

6. What are some relevant Web sites for this material?

Using your favorite search engine, and maybe one or two others, type in a few key words such as "linear inequality" or "graphing linear inequality" or "solving linear inequality" .

Here are four Web sites that I liked:

• http://www.purplemath.com/modules/ineqgrph.htm
• http://www.wtamu.edu/academic/anns/mps/math/mathlab/beg_algebra/beg_alg_tut24_ineq.htm
• http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut22_linineq.htm
• http://www.regentsprep.org/Regents/math/math-topic.cfm?TopicCode=solvin

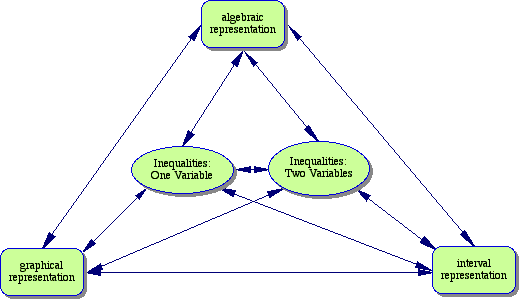
7. What concept map can I create for this section?

8. What types of Mathematica activities can I create?

Mathematica can produce plots for a set of inequalities that are far more complex than one would normally try to envisage by manual means. Even if one does not have Mathematica, seeing a few examples of such plots can expand one's imagination of what is possible.

9. What are some connections to other ideas?

The idea of an inequality is simply an extension of the idea of an equation. Instead of finding a value of an unknown variable that satisfies an equation, one tries to find all of the values of a variable that are less than a particular equation.

10. What is my overall reaction to this section?

This is a very short and simple section. There are only a couple of new ideas, and they involve notation more than some type of complex manipulation of symbols.

11. Comments on Dyer: 2. Living the Paradoxical Mystery

This section discusses the idea of thinking of dichotomies such as beauty - ugly as a continuum and that everything has a varying amount of both. In the case of mathematics one such continuum might be easy - hard. But nothing is easy, or hard. Rather an item or situation has varying degrees of both, depending in large upon the previous background of the individual. Even the idea of a single dimension is restrictive, both in reality as well as in mathematics. Everything is highly multidimensional. Within mathematics this should be an automatic extension of most topics. If this is an idea in 2-dimensions, can it be extended to 3-dimensions? Or 4, or more generally, to n-dimensions, where n is a positive integer? What about fractional dimensions? Is there a way that it makes sense to consider this? (The answer to the last question is, surprisingly, sometimes yes. This is a topic within the general area of fractal geometry and non-linear dynamics, also referred to as chaos theory.)