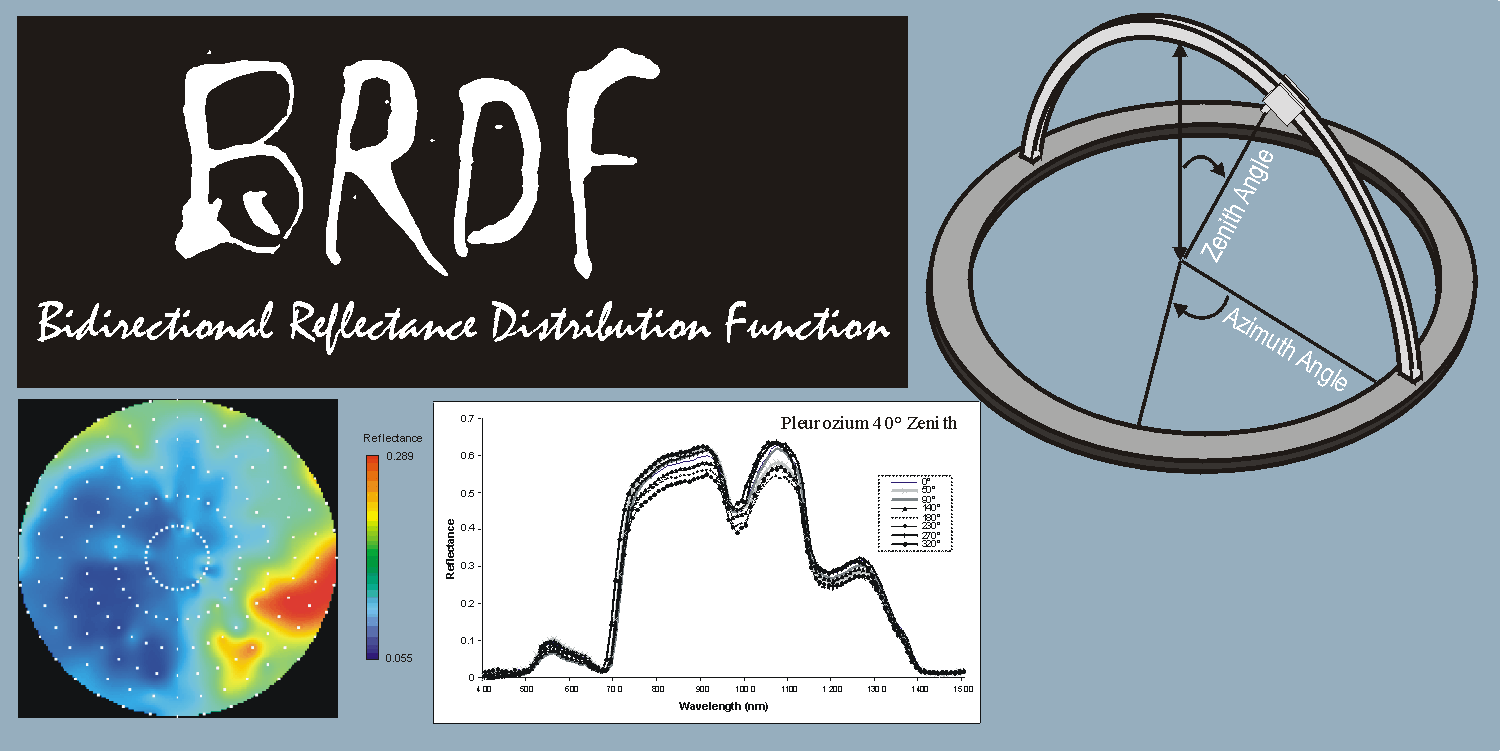

The purpose of this page is to provide some insight into the complex world of surface reflectance. The data presented here were acquired with the University of Lethbridge Goniometer System (ULGS). The ULGS represents a low-cost solution to the problem of measuring angular surface reflectance developed in collaboration with Dr. Derek Peddle. Research into the bi-directional nature of surface reflectance is relatively new in the field of remote sensing and knowledge of these specific surface interactions will help us understand the nature of satellite image data and provide improved information for environmental models that use the BRDF of surfaces as input.
The central concept that has underpinned the field of remote sensing is the spectral signature. A spectral signature is a record of the unique reflectance properties of a surface. If we have sufficient knowledge about the way a surface interacts with incident electromagnetic energy (reflects or absorbs) then we should be able to distinguish features based on their reflectance pattern alone. In theory, this concept was sound and in practice, many features when measured at close distances can be distinguished based on spectral response alone (e.g. water from vegetation etc.). The spectral signature concept is sufficient for describing simple interactions (reflectance and absorption) but does not seek to characterize the variation that can occur in spectral response when the reflecting surface is not perfectly diffuse (Lambertian). In effect, what you see depends not only on the spectral response, but on the view direction.
The classic example used to demonstrate this effect is the pattern seen on the grass of golf courses and baseball diamonds after they are mowed.
This specification of comprehensive multi-angular reflectance information is typically gathered in the form of the Bidirectional Reflectance Distribution Function (BRDF) in which the magnitude of reflectance is obtained at all (zenith and azimuth) angles throughout the viewing hemisphere. However, since it is essentially impossible to measure reflectance at all angles, the BRDF is instead estimated as a function of multiple reflectance information obtained at discrete angles. In the field, and also in laboratory settings, the direct estimation of BRDF is achieved with the aid of a goniometer – an instrument that positions a sensor to acquire spectral measurements over a full range of viewing angles. The resulting BRDF of a target yields important information about the physical structure of the target that cannot be generated from single-angle spectral measurements (Barnsley et al., 1994; Combal et al, 2002).
The measurement of BRDF has been an increasingly important component in support of studies that seek to characterize earth surface features from remotely sensed data (Barnsley et al., 1994). For example, the derivation of biophysical variables such as leaf area index (LAI), biomass, net primary productivity and fraction of absorbed photosynthetically active radiation (fAPAR) from remotely sensed data would be improved if a true estimate of the canopy BRDF was known (Combal, et al, 2002, Sandmeier and Deering, 1999).
With the development of airborne (e.g. ASAS, casi) and satellite (e.g. SPOT, MISR) sensors capable of off-nadir imaging, as well as the across-track capabilities of sensors with wide field of views such as MODIS and AVHRR, a relatively coarse estimation of surface BRDF is possible (Barnsley et al., 1994). These sensors, and future designs with similar or improved capabilities, will be expected to provide more accurate characterizations of the surface BRDF and allow for improved estimates of biophysical parameters by taking advantage of angular reflectance information.
The estimation of BRDF using ground instruments will become increasingly important for the validation of these remote sensing image products and canopy BRDF models towards developing a more thorough understanding of the physical controls and spectral and angular properties of various targets (Sandmeier, 2000). However, the main constraints in gathering these data are the cost and availability of instruments to perform the measurements (Sandmeier and Itten, 1999).
Barnsley, M.J., Strahler, A.H., Morris, K.P., and Muller, J.P. 1994. Sampling the surface bidirectional reflectance distribution function (BRDF): 1. Evaluation of current and future satellite sensors. Remote Sensing Reviews Vol.8, pp 271-311.
Combal, B., Baret, F., Weiss, M., Trubuil, A., Macé, D., Pragnère, A., Myneni, R., Knyazikhin Y., and Wang L. 2002. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem.
Remote Sensing of Environment, Vol. 84, pp.1-15.
Nicodemus, F., E., Richmond, J., C., Hsia, J., J., Ginsberg, I., W., and Limperis, T., 1977. Geometrical considerations and nomenclature for reflectance. Technical Report NBS MN-160, National Bureau of Standards.
Peddle, D.R., H.P. White, R.J. Soffer, J.R. Miller and E.F. LeDrew, 2001.
Reflectance processing of remote sensing spectroradiometer data. Computers & Geosciences. Vol. 27, pp. 203-213.
Sandmeier, S., Itten, I., K., 1999. A field goniometer system (FIGOS) for acquisition of hyperspectral BRDF data. IEEE Transactions on Geoscience and Remote Sensing, Vol. 37, pp. 978 – 986.
Sandmeier, S. 2000. Acquisition of Bidirectional Reflectance Factor Data with Field Goniometers. Remote Sensing of Environment. Vol. 73, pp. 257-269.
So what is BRDF?
Historical Perspective.
In remote sensing we are primarily concerned with gathering data from objects from a distance. Over time the science of remote sensing has progressed from visual interpretation of aerial photographs to advanced satellite sensing systems. The development of these systems has enabled us to view the Earth’s surface from a myriad of different regions of the electromagnetic spectrum and at spatial resolutions from sub-meter to kilometers. The data recorded by these instruments has proven invaluable in the earth and environmental sciences and as we continue to expand our views of the Earth, we are increasingly interested in the variety of information that these sensors can provide aside from simple spectral and spatial analysis. 
When this grass is mowed, it is rolled so that the blades of grass are all oriented in the same direction. Consecutive passes produce alternating light and dark stripes of grass. This is caused by the grass leaf structure and the relationship between the leaf, sun, and sensor. The grass plant is therefore not reflecting the incident radiation equally with respect to direction, causing it to look different; this is the effect of bi-directional reflectance.
Angular Remote Sensing
One of the central concepts in remotes sensing is reflectance. Reflectance is an inherent property of a surface, and is independent of time, location, illumination intensity, atmospheric conditions and weather (Peddle et al., 2001). If the surface is perfectly Lambertian in nature (it reflects incident energy equally in all directions) then reflectance is invariant with respect to view angle (it’s colour doesn’t change no matter what angle you look at it.). Unfortunately we don’t live in a Lambertian world and surfaces tend to reflect incident energy preferentially. So a surface can not be simply characterized by its reflectance, but we also need to characterize preferential distribution. This leads to the Bidirectional Reflectance Distribution Function. Information about angular reflectance characteristics of non-Lambertian surfaces from a variety of illumination and view angles is important for their correct characterization with respect to fundamental spectral signature development, experimental validation, surface modeling and various forms of image analysis accuracy assessment.
BRDF Defined
The estimation of the Bidirectional Reflectance Distribution Function (BRDF) was defined by Nicodemus et al. (1977) as the intrinsic property of a surface that describes the angular distribution of radiation reflected by the surface for all angles of exitance and under any given illumination geometry. The BRDF of a surface is, by definition, infinitesimal and, therefore, all direct measurements are approximations of the BRDF function (1): 
Where dL is the differential radiance, dE is the differential incident irradiance for a given zenith angle (theta) and azimuth angle (rho), for any wavelength (lambda) (Figure 1).

Reference: