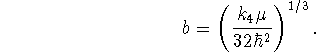Chemistry 3730 Spring 1997 Test 2 Solutions

1. Here is a rough sketch of the spectrum:

   

   The fundamental spectrum is centered on ; these lines are due to transitions during which the vibrational quantum number is changed by . The first overtone is centered on (corresponding to transitions during which the vibrational quantum number changes by 2) and additional overtones (of decreasing intensity and similar structure) are potentially observable at for integer values of j. The intensity of each overtone is lower than that of the previous because overtones violate the harmonic oscillator selection rule which is approximately obeyed for vibrational states. Each line corresponds to a transition from a different rotational state. Lines to the left (high-energy) side of the centre correspond to transitions during which the rotational quantum number increases. Lines lower in energy than the centre of the fundamental or overtone correspond to transitions during which the rotational quantum number decreases.

2. . There are only two unpaired electrons but germanium has a valence of four. Germanium can form four bonds by promotion of an s electron to a p orbital.
3. There are four angular momenta in this problem, namely the orbital and spin angular momenta of each of the two electrons. An s electronic state has an orbital angular momentum quantum number of 0 while a p state has . The electron's spin is of course .

   Let's start by adding up the orbital angular momenta. The quantum number for the total orbital angular momentum can be anything between 1-0 and 1+0. In other words, this quantum number can only be 1.

   The total spin quantum number can be either or , i.e. either 0 or 1.

   If the total spin quantum number is zero, the total angular momentum quantum number must be 1. If the total spin quantum number is 1, the total angular momentum quantum number can be any number between 1-1 and 1+1 in steps of 1. Thus the possible values of the total angular momentum quantum number are 0, 1 and 2.

4. Electrons are light, fast-moving particles. Nuclei are much heavier and move much more slowly. Accordingly, the nuclei can only react to the average electron density rather than to the detailed motions of the electrons. Conversely, the nuclei appear to be frozen in place from the perspective of the electrons. This separation of timescales allows us to separate the molecular problem into two subproblems, one for the electrons and one for the nuclei.

   On the timescale of motion of the electrons, nuclear motion is exceedingly slow. Thus nuclear-nuclear repulsion terms are effectively constant. Furthermore, since the nuclear wavefunction is relatively strongly localized, nuclear kinetic energy terms are zero almost everywhere. We can therefore reduce the electronic Hamiltonian to

   

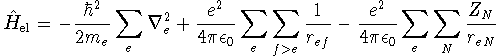
   where lower case subscripts label electrons and upper case subscripts label nuclei. The dependence of the electronic wavefunctions and energies on the nuclear positions enters parametrically through the electron-nuclear attraction terms. We solve the electronic problem for several different nuclear geometries (different bond lengths and angles). For each geometry, we obtain a series of electronic energies. Each electronic state therefore corresponds to an energy hypersurface parameterized by the nuclear coordinates.

   After solving the electronic problem, the molecular Hamiltonian becomes

   

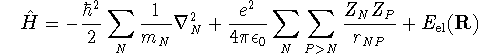
   where is the vector of nuclear coordinates. If we add the last two terms, we get the effective potential energy ( ) experienced by the nuclei. Thus nuclear motion obeys the Schrödinger equation

   

   where

   

5. The kinetic energy operator is . The average is found by .
   

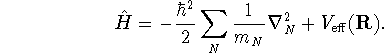
   > assume(b>0);
   > avgK := -hbar^2/(2*mu)*sqrt(b/Pi)
   > *int(exp(-b*x^2/2)*diff(exp(-b*x^2/2),x$2),
   > x=-infinity..infinity);

   

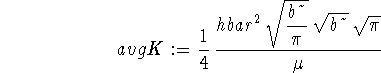
   > simplify(avgK);

   

   
   

   I carried out the next step using an advanced Maple command (subs()), but this could equally well have been done by hand.
   

   > subs(b=sqrt(k*mu)/hbar,");

   

   
   

   This is , or half the ground state energy. Incidentally, this is an example of the virial theorem. For potentials which are homogeneous functions of their arguments (functions for which ), the average kinetic energy is always a simple multiple of the total energy.

6. This is a variational problem. The Hamiltonian is .

   Let's start by defining the wavefunction:
   

   > phi:=x->exp(-b*x^2);

   

   
   

   The variational energy is . Let's compute it one part at a time:
   

   > top:=int(phi(x)*(-hbar^2/(2*mu)*diff(phi(x),x$2)
   > +k4*x^4/24*phi(x)),x=-infinity..infinity);

   

   > bottom:=int(phi(x)^2,x=-infinity..infinity);

   

   > Evar := simplify(top/bottom);

   

   
   

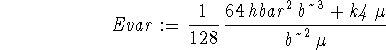
   To find the best value of b, we minimize the variational energy with respect to b:
   

   > sol:=solve(diff(Evar,b)=0,b);

   

   
   

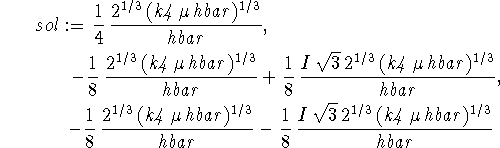
   Only the first of these solutions is physically reasonable. Again, I'm going to use subs() to do the work, although you probably worked out these parts of the problem by hand.
   

   subs(b=sol[1],Evar);

   

   
   

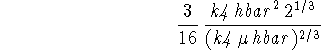
   The normalization factor is .
   

   > sqrt(1/bottom);

   

   
   

   Thus the normalized wavefunction is

   

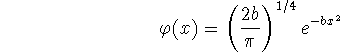
   with