Chemistry 3730 Fall 1998 Test 2 Solutions

1. Technetium is element number 43.

   

2. The noble gas preceding Tc is Kr. The ground-state electronic configuration of Tc is therefore

   

3. The vibrational frequency is inversely proportional to . The reduced mass is approximately equal to the mass of the lighter element in a diatomic molecule when there is a large mass difference. Accordingly, the reduced mass of is about three times larger than the reduced mass of so the vibrational frequency is reduced by a factor of . The fundamental vibrational frequency of should therefore be about .
4. To calculate the average potential energy, we need the inner product

   

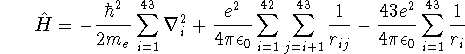
   > psi2 := x -> (2*alpha/Pi)^(1/4)*(4*alpha*x^2-1)*exp(-alpha*x^2);

   

   > V := x -> 1/2*k*x^2;

   

   > assume(alpha>0);
   > int(psi2(x)^2*V(x),x=-infinity..infinity);

   

   If we substitute the value of into this expression and simplify, we get . This is exactly half the energy of this state.

5. The average value of is obtained by

   

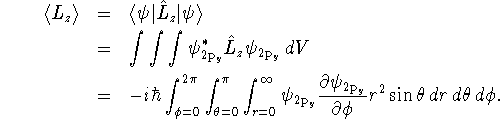
   > psi2py := (r,theta,phi) ->
   > 1/sqrt(32*Pi*a0^5)*r*exp(-r/(2*a0))*sin(theta)*sin(phi);

   

   > assume(a0>0);
   > -I*hbar*int(int(int(psi2py(r,theta,phi)
   > *diff(psi2py(r,theta,phi),phi)*r^2*sin(theta),theta=0..Pi),
   > phi=0..2*Pi),r=0..infinity);

   

   Bonus: We obtain real-valued wavefunctions by adding or subtracting wavefunctions with equal and opposite values of . The resulting wavefunctions are of the form

   

   where N is a normalization constant ( ) and the original wavefunctions are assumed to be normalized. The average value of is obtained by

   

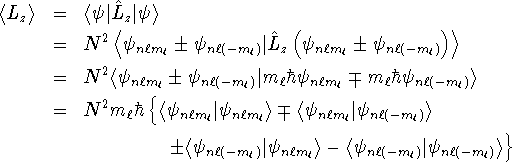
   The inner products and are both zero because they are inner products of wavefunctions which are eigenfunctions of a Hermitian operator ( ) corresponding to different eigenvalues. The other two are normalization integrals so they are both equal to 1. Therefore .

6. The variational wavefunction is

   > phi := x -> sin(Pi*x/L) + a*sin(Pi*x/L)^2;

   

   We compute the variational energy in pieces.

   > Kip := -hbar^2/(2*m)*int(phi(x)*diff(phi(x),x$2),x=0..L);

   

   > V := x -> k/2*(x-L/2)^2;

   

   > Vip := int(phi(x)^2*V(x),x=0..L);

   

   > ip := int(phi(x)^2,x=0..L);

   

   Let us define the parameters before proceeding any further:

   > k:=0.002;

   

   > m:=1e-26;

   

   > L:=0.3e-9;

   

   > h := 6.6261e-34;

   

   > hbar := h/(2*Pi);

   

   We can now compute the variational energy:

   > Evar := (Kip+Vip)/ip;

   

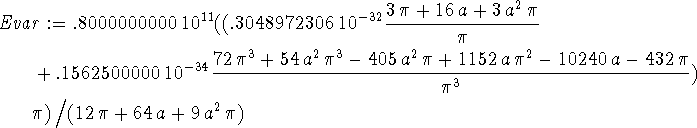
   > sa:=solve(diff(Evar,a)=0,a);

   

   > Evar1 := evalf(subs(a=sa[1],Evar));

   

   > Evar2 := evalf(subs(a=sa[2],Evar));

   

   Evar2 is the lower energy so it is our approximation to the ground-state energy. Note that the corresponding value of a is small and that the first part of the variational wavefunction is just a particle-in-a-box wavefunction. This means that the solution is very much like that of the particle-in-a-box problem and, by implication, less like the solution of the harmonic oscillator.