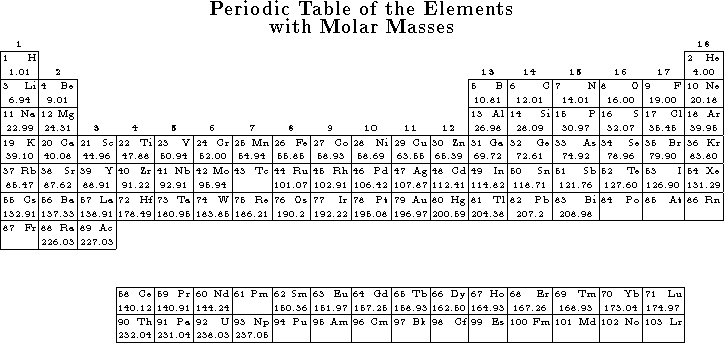
![]()
with ![]() .
Give your answer in terms of
.
Give your answer in terms of ![]() and
and ![]() .
On average, what fraction of the total energy is potential?
[10 marks]
.
On average, what fraction of the total energy is potential?
[10 marks]
Maple hints: ![]() is Pi in Maple and
is Pi in Maple and ![]() is exp(x). Do the calculation without defining
is exp(x). Do the calculation without defining
![]() . Maple will need to know that
. Maple will need to know that ![]() is a positive
constant however. It is probably easiest to complete the
calculation by hand.
is a positive
constant however. It is probably easiest to complete the
calculation by hand.
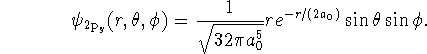
In spherical polar coordinates, the operator ![]() is
is
![]()
Calculate the expectation value of ![]() for the
for the ![]() state of a hydrogen atom.
[10 marks]
state of a hydrogen atom.
[10 marks]
Maple hints: The function ![]() is typed exp(x) in
Maple and
is typed exp(x) in
Maple and ![]() is sqrt(y). The number
is sqrt(y). The number ![]() is
Pi and the imaginary unit i is I.
Maple will need to know that
is
Pi and the imaginary unit i is I.
Maple will need to know that ![]() is a positive
constant.
is a positive
constant.
Bonus: From the method by which real-valued
wavefunctions such as the
![]() are obtained and the properties of
inner products, prove that the result obtained above is
generally true.
are obtained and the properties of
inner products, prove that the result obtained above is
generally true.
![]()
This is a harmonic oscillator with hard walls to either side.
Suppose that ![]() ,
, ![]() and
and ![]() .
Compute an approximation to the ground-state energy using
the variational wavefunction
.
Compute an approximation to the ground-state energy using
the variational wavefunction
![]()
Is this model with the given parameters more like a harmonic oscillator or is it more like a particle in a box? Explain briefly. [15 marks]
Maple hints:
The number ![]() is
Pi in Maple. Type all numerical values needed to solve
this problem into your Maple session after after you have
calculated the integrals. Use subs() to substitute
values of the variational parameter into the variational energy.
is
Pi in Maple. Type all numerical values needed to solve
this problem into your Maple session after after you have
calculated the integrals. Use subs() to substitute
values of the variational parameter into the variational energy.
Note: We are imagining here a single mass connected by springs
to immovable walls so ![]() , the mass of the particle.
, the mass of the particle.
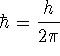
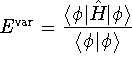
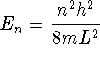 where
where
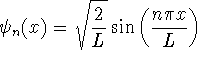
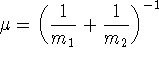 .
.