Assignment 9

Due: 10:00 a.m., Wednesday, Nov. 25

In this assignment, we will take a second look at the ``oscillator-in-a-box'' problem studied in the last test. In the oscillator-in-a-box problem, a particle of mass m is connected by a pair of springs of effective harmonic force constant k to two hard walls separated by a distance L. Thus the potential energy is

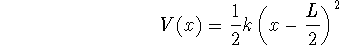
with the constraint .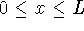

Our solution technique will be Fourier synthesis: In Fourier synthesis, we construct an unknown function from a sum of trigonometric functions. In this case, we will use particle-in-a-box (sine) functions as our basis states (because they satisfy the boundary conditions) so we will write the variational wavefunction in the form

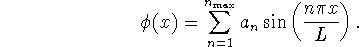
1. Define the following quantities in your Maple session: 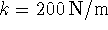, , 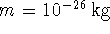and 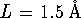. Also enter a numeric value for .
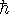2. First take 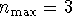. For convenience, we can set 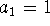while working out the variational problem. Find an approximation to the ground-state energy using this variational wavefunction. If you do everything correctly, you will get several solutions for 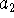and 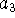. The best one will have a very small value of 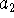. This is because the basi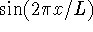s function has the wrong parity for the ground state of this problem: As in the particle-in-a-box and harmonic oscillator problems, the ground-state wavefunction for the oscillator in a box is symmetric about the center of the potential well. The basis function 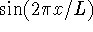is antisymmetric so it does not contribute to the solution.

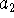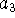   Maple hints: To solve a pair of equations in two unknowns, type solve({eq1,eq2},{a,b}); where eq1 and eq2 are the equations and a and b are the unknowns. Note that this may take a while. Use subs() to substitute values of and into your variational energy.

3. Since antisymmetric basis states do not contribute to the ground-state wavefunction, repeat the last set of calculations leaving out the 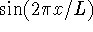term. Does this improve the energy at all?
4. Do a variational calculation with the Fourier trial wavefunction with 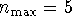but leave out all the even-numbered terms. Again, you can set 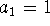. Find the variational energy for this wavefunction. Which is the best wavefunction of the three you have tried?
5. Normalize and plot the best wavefunction you found.
6. Compare this wavefunction to the ground-state harmonic oscillator wavefunction and to the ground-state particle-in-a-box wavefunction. The harmonic oscillator wavefunction for a particle of mass m tethered to an immovable wall is

   

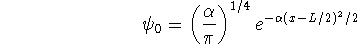
   where 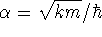. Does the variational wavefunction ressemble one or the other more?

Bonus:

Find an approximation to the energy of the first excited state using Fourier synthesis for the variational wavefunction. Normalize and plot your approximate wavefunction for this state.

Hint: Your wavefunction should have the correct parity.