Assignment 8 solutions

1. 1. The wavefunction is

      > psi2px := (r,theta,phi) ->
      > N*r*exp(-r/(2*a0))*sin(theta)*cos(phi);

      

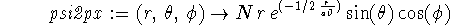
      where N is a normalization constant. We wish to find a value of N such that .

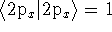      > assume(a0>0);
      > solve(int(int(int(psi2px(r,theta,phi)^2*r^2*sin(theta),
      > phi=0..2*Pi),theta=0..Pi),r=0..infinity)=1,N);

      

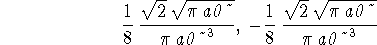
      > N:=1/8*sqrt(2)*sqrt(Pi*a0)/(Pi*a0^3);

      

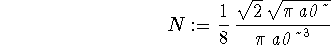
      Verification:

      > int(int(int(psi2px(r,theta,phi)^2*r^2*sin(theta),phi=0..2*Pi),
      > theta=0..Pi),r=0..infinity);

      

   2. The average kinetic energy is 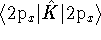. Because K involves the Laplacian and the Laplacian is complicated, it's easiest to do this in pieces:

      

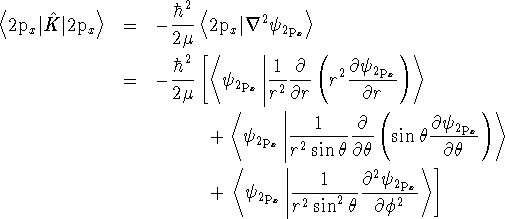
      > Lrip := int(int(int(psi2px(r,theta,phi)*1/r^2
      > *diff(r^2*diff(psi2px(r,theta,phi),r),r)*r^2*sin(theta),
      > phi=0..2*Pi),theta=0..Pi),r=0..infinity);

      

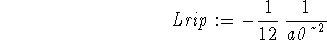
      > Ltip := int(int(int(psi2px(r,theta,phi)*1/(r^2*sin(theta))
      > *diff(sin(theta)*diff(psi2px(r,theta,phi),theta),theta)
      > *r^2*sin(theta),phi=0..2*Pi),theta=0..Pi),r=0..infinity);

      

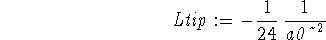
      > Lpip := int(int(int(psi2px(r,theta,phi)*1/(r^2*sin(theta)^2)
      > *diff(psi2px(r,theta,phi),phi$2)*r^2*sin(theta),phi=0..2*Pi),
      > theta=0..Pi),r=0..infinity);

      

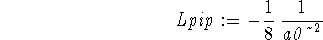
      > K_avg := -hbar^2/(2*mu)*(Lrip+Ltip+Lpip);

      

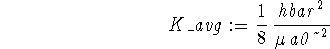
   3. We first need to calculate the radial probability density.

      > rpd2p := int(int(psi2px(r,theta,phi)^2*r^2*sin(theta),
      > phi=0..2*Pi),theta=0..Pi);

      

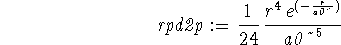
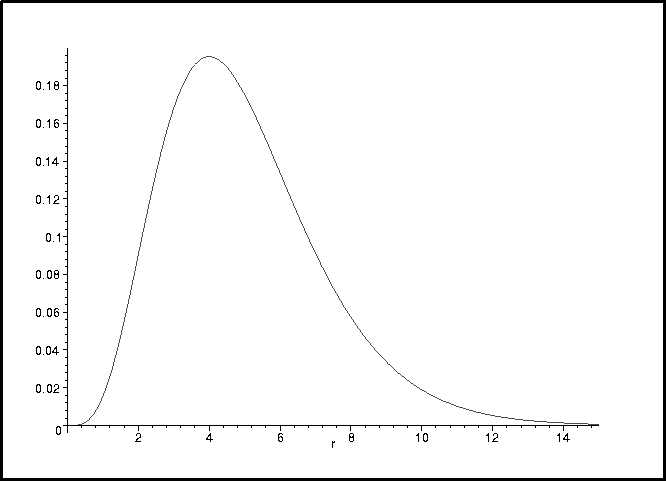
      > plot(subs(a0=1,rpd2p),r=0..15);

      
   4. We could do a triple integral of the square of the wavefunction, but we have already done two of the required integrals when we calculated the radial probability density so we can just use that to simplify the calculation:

      > evalf(int(rpd2p,r=2*a0..infinity));

      

2. 1. > V := x -> Ea*((x/xe)^2-1)^2;

      

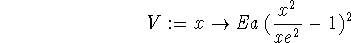
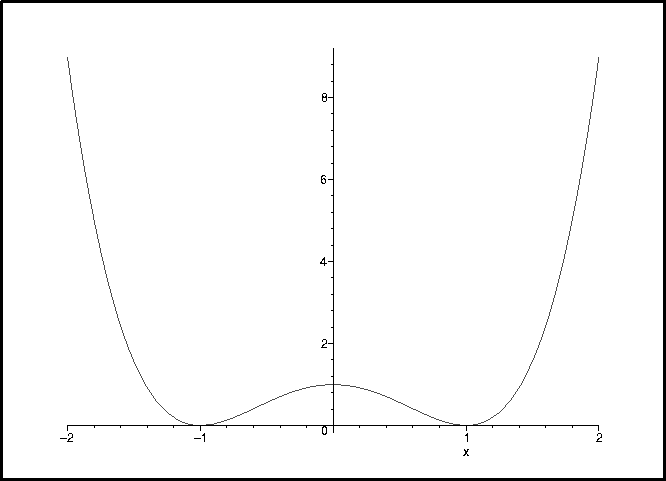
      > plot(subs(xe=1,Ea=1,V(x)),x=-2..2);

      

   2. 

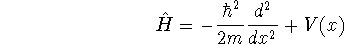
   3. phi := x -> exp(-b*(x-xe)^2)+exp(-b*(x+xe)^2);

      

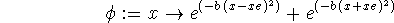
      As usual, we compute the variational energy in pieces. Note the use of colons instead of semi-colons to suppress unwanted screen output.

      > assume(b>0);
      > Kip := -hbar^2/(2*m)*int(phi(x)*diff(phi(x),x$2),
      > x=-infinity..infinity):
      > Vip := int(phi(x)^2*V(x),x=-infinity..infinity):
      > ip := int(phi(x)^2,x=-infinity..infinity):
      > Evar := (Kip+Vip)/ip:
      > best_b:=solve(diff(Evar,b)=0,b);

      

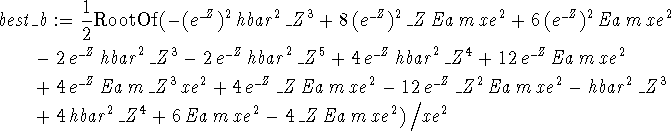
   4. > Ea := 50e3/6.0221e23;

      

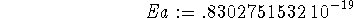
      > xe := 2e-10;

      

      > m := 1.6726486e-27;

      

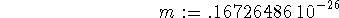
      > hbar := 6.6261e-34/(2*Pi);

      

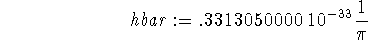
      > evalf(best_b);

      

      > E0:=evalf(subs(b=%,Evar));

      

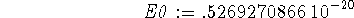
   5. > xl := solve(V(x)=E0,x);

      

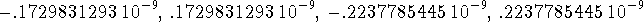
      The first two solutions are the left and right extremes of the barrier while the other two are the left and right outer classical turning points.

      We need a normalized wavefunction to evaluate probabilities:

      > nf := 1/sqrt(int(subs(b=bb,phi(x)^2),x=-infinity..infinity));

      

      > phin:=x->phi(x)*nf;

      

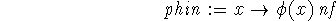
      Verification:

      > evalf(int(subs(b=bb,phin(x)^2),x=-infinity..infinity));

      

      > evalf(int(subs(b=bb,phin(x)^2),x=xl[1]..xl[2]));

      

      This probability is actually quite large so tunneling through the barrier must be a significant event.