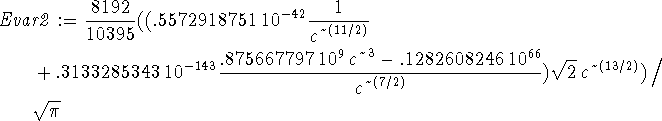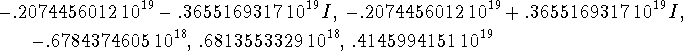Assignment 7 solutions

1. The potential energy is

   > V := r -> epsilon*((sigma/r)^12-(sigma/r)^6);

   

   > epsilon := 1.71e-21;

   

   > sigma := 342e-12;

   

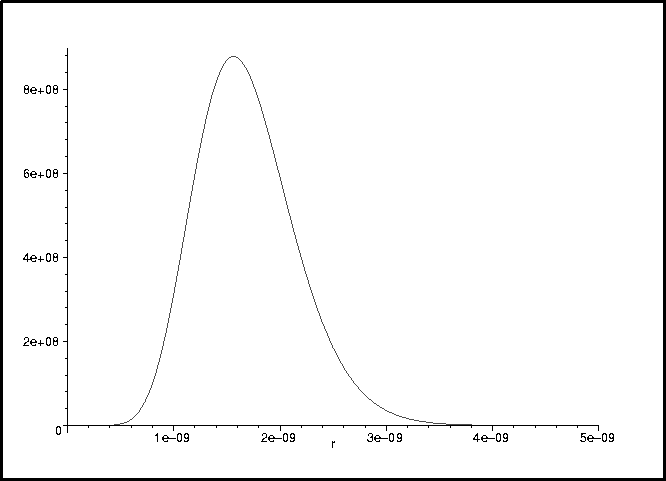
   > plot(V(r),r=0..1e-9,-1e-21..1e-21);

   
2. The Hamiltonian is

   

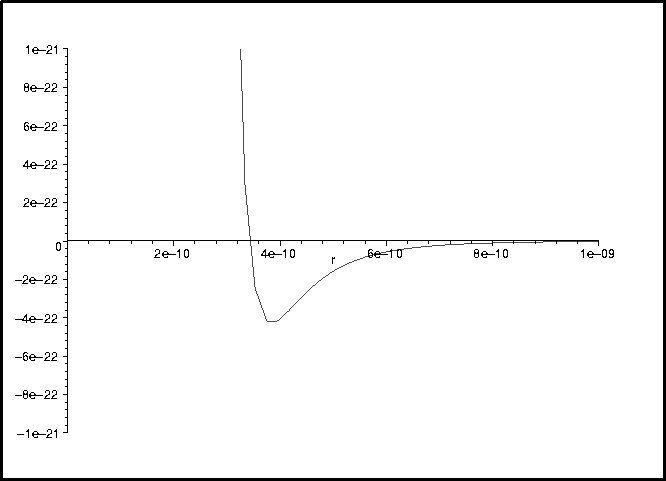
   The mass of one argon atom, in kg, is

   > mAr := 39.962384/1000/6.02214e23;

   

   The reduced mass of two argon atoms is therefore

   > mu := 1/(1/mAr+1/mAr);

   

   We also need :

   > hbar := 6.62608e-34/(2*Pi);

   

3. Define the trial wavefunction:

   > phi := r -> r^6*exp(-b*r);

   

   > assume(b>0);

   The variational energy is . We do the calculation in pieces:

   > Kip := int(phi(r)*(-hbar^2/(2*mu))*diff(phi(r),r$2),r=0..infinity);

   

   > Vip := int(phi(r)*V(r)*phi(r),r=0..infinity);

   

   > ip := int(phi(r)^2,r=0..infinity);

   

   > Evar:=(Kip+Vip)/ip;

   

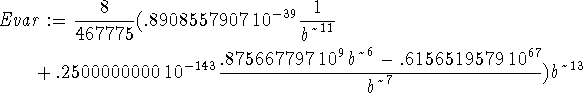
   The best wavefunction minimizes the variational energy. In this calculation, the variational parameter is b so we want to minimize with respect to b.

   > solve(diff(Evar,b)=0,b);

   

   We want a real, positive b. (It is possible for b to be complex with a positive real part. However, if you try substituting the complex solutions into the variational energy, you will find that in this case they all give complex energies. Complex energies are nonsense so these complex roots are all spurious.) There are only two roots which might possibly be right. The best one gives the lowest energy.

   > subs(b=2109144137.,Evar);

   

   > subs(b=3839407642.,Evar);

   

   The second solution gives the lower energy so it is the right one. Note in fact that the first value of b tried gives a positive energy. This is the equivalent, for intermolecular forces, of an antibonding state.

4. From here on in, we want to use the best value of b:

   > b := 3839407642;

   

   The normalized wavefunction is calculated by

   > ip := int(phi(r)^2,r=0..infinity);

   

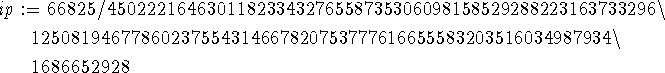
   > phi_normalized := r -> phi(r)/sqrt(ip);

   

   Verification:

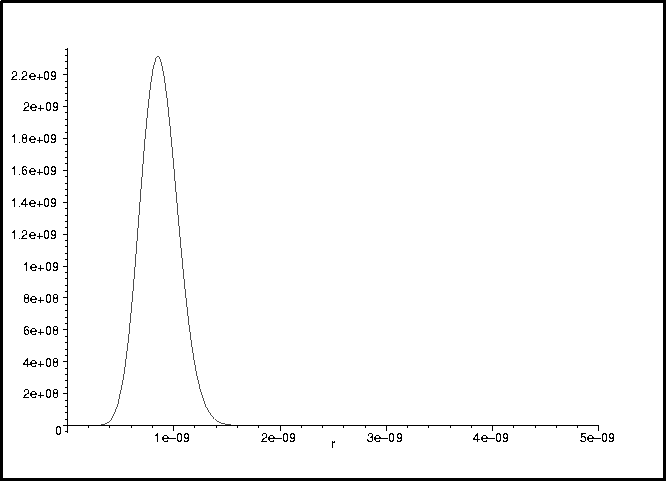
   > int(phi_normalized(r)^2,r=0..infinity);

   

5. > plot(phi_normalized(r)^2,r=0..5e-9);

   

Bonus 1:

The work which must be done is very similar to what we had to do above, except that we're using a different trial wavefunction.

> phi2 := r -> r^6*exp(-c*r^2);

> assume(c>0);
> Kip2 := int(phi2(r)*(-hbar^2/(2*mu))*diff(phi2(r),r$2),r=0..infinity);

> Vip2 := int(phi2(r)*V(r)*phi2(r),r=0..infinity);

> ip2 := int(phi2(r)^2,r=0..infinity);

> Evar2:=(Kip2+Vip2)/ip2;

> solve(diff(Evar2,c)=0,c);

> evalf(subs(c=.6813553329e18,Evar2));

> evalf(subs(c=.4145994151e19,Evar2));

The second solution is the correct one. Furthermore, this energy is much lower than the energy obtained with the other trial wavefunction so this is a better variational wavefunction. Let's have a look at it:

> c := .4145994151e19;

> ip2 := int(phi2(r)^2,r=0..infinity);

> phi2_n := r -> phi2(r)/sqrt(ip2);

Verification:

> int(phi2_n(r)^2,r=0..infinity);

The small difference from 1 is just round-off error.

> plot(phi2_n(r)^2,r=0..5e-9);

Note that that probability maximum occurs at much smaller r for this wavefunction. This is because the first form we tried did not fall off sufficiently quickly at larger r. This kind of observation is often use to guess at good forms for variational wavefunctions.