> psi := (nx,ny,Lx,Ly,x,y) -> > 2/sqrt(Lx*Ly)*sin(nx*Pi*x/Lx)*sin(ny*Pi*y/Ly);
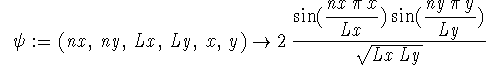
For 
:
> int(int(psi(1,1,Lx,Ly,x,y)^2,x=0..Lx/3),y=Ly/4..Ly/2);
> evalf(%);
For 
, 
:
> int(int(psi(1,2,Lx,Ly,x,y)^2,x=0..Lx/3),y=Ly/4..Ly/2);
> evalf(%);
For 
, 
:
> int(int(psi(2,1,Lx,Ly,x,y)^2,x=0..Lx/3),y=Ly/4..Ly/2);
> evalf(%);
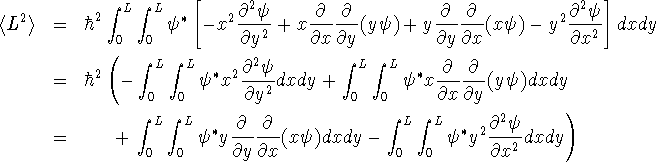
I'll start with the (1,7) state. I'll calculate the four integrals separately and then add them up at the end.
> i17_1 := -int(int(psi(1,7,L,L,x,y)*x^2*diff(psi(1,7,L,L,x,y),y$2), > x=0..L),y=0..L);
> i17_2 := int(int(psi(1,7,L,L,x,y)*x > *diff(diff(y*psi(1,7,L,L,x,y),y),x),x=0..L),y=0..L);
> i17_3 := int(int(psi(1,7,L,L,x,y)*y > *diff(diff(x*psi(1,7,L,L,x,y),x),y),x=0..L),y=0..L);
> i17_4 := -int(int(psi(1,7,L,L,x,y)*y^2*diff(psi(1,7,L,L,x,y),x$2), > x=0..L),y=0..L);
> L2_17 := hbar^2*(i17_1+i17_2+i17_3+i17_4);
Now for the (7,1) state:
> i71_1 := -int(int(psi(7,1,L,L,x,y)*x^2*diff(psi(7,1,L,L,x,y),y$2), > x=0..L),y=0..L);
> i71_2 := int(int(psi(7,1,L,L,x,y)*x > *diff(diff(y*psi(7,1,L,L,x,y),y),x),x=0..L),y=0..L);
> i71_3 := int(int(psi(7,1,L,L,x,y)*y > *diff(diff(x*psi(7,1,L,L,x,y),x),y),x=0..L),y=0..L);
> i71_4 := -int(int(psi(7,1,L,L,x,y)*y^2*diff(psi(7,1,L,L,x,y),x$2), > x=0..L),y=0..L);
> L2_71 := hbar^2*(i71_1+i71_2+i71_3+i71_4);
Note that this is exactly the same as 
for the (1,7)
state. This is not surprising since the (1,7) and (7,1) states are
related by interchange of the axis labels, so any observables which
don't depend on this choice should be exactly the same for both
states.
Finally, for the (5,5) state:
> i55_1 := -int(int(psi(5,5,L,L,x,y)*x^2*diff(psi(5,5,L,L,x,y),y$2), > x=0..L),y=0..L);
> i55_2 := int(int(psi(5,5,L,L,x,y)*x > *diff(diff(y*psi(5,5,L,L,x,y),y),x),x=0..L),y=0..L);
> i55_3 := int(int(psi(5,5,L,L,x,y)*y > *diff(diff(x*psi(5,5,L,L,x,y),x),y),x=0..L),y=0..L);
> i55_4 := -int(int(psi(5,5,L,L,x,y)*y^2*diff(psi(5,5,L,L,x,y),x$2), > x=0..L),y=0..L);
> L2_55 := hbar^2*(i55_1+i55_2+i55_3+i55_4);
