> int((x-2)*exp(-x^3),x=0..5);
![]()
> evalf(%);
![]()
> ts := x -> tan(sin(x));
![]()
> plot(ts,0..2*Pi);
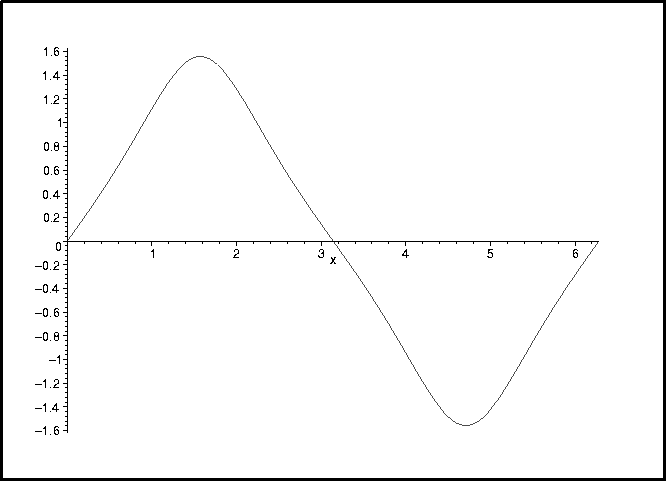
> solve(ts(x)=1,x);
![]()
> int((x-2)*exp(-x^3),x=0..5);
![]()
> evalf(%);
![]()
> ts := x -> tan(sin(x));
![]()
> plot(ts,0..2*Pi);

> solve(ts(x)=1,x);
![]()
I expected you to try to find the second solution which you can see on the graph of your function. Let's think about this for a second. The sine function looks like:
> plot(sin(x),x=0..2*Pi);
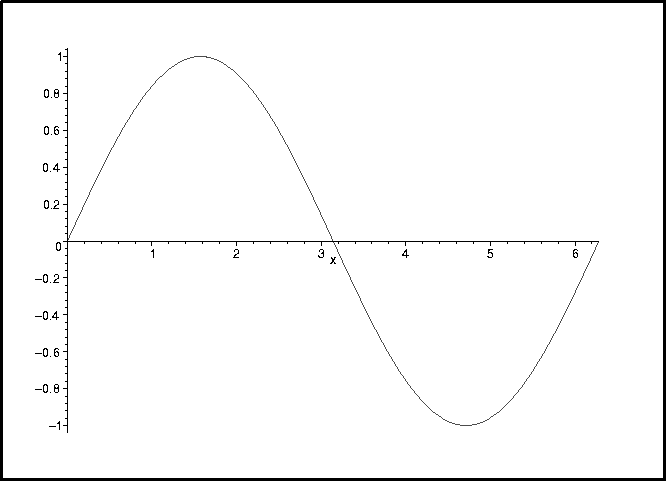
The reason why there are two solutions should now be clear: Between 0
and ![]() ,
, ![]() passes through every value between 0 and 1
twice. We just have to find a solution to the equation
passes through every value between 0 and 1
twice. We just have to find a solution to the equation
![]() with
with ![]() :
:
> u:=arcsin(Pi/4);
![]()
> solve(sin(u)=sin(u+a),a);
![]()
Maple finds two solutions, one of which is obvious and unhelpful (0). The other one is the one we want. Let's call the second solution of the equation w:
w:=arctan(Pi*sqrt(16-Pi^2)/(-8+Pi^2))+u;
![]()
Let's verify this result. First of all, we'll look at the floating-point value of w and make sure that it makes sense:
> evalf(w);
![]()
Comparing this value to the approximate solution found by examining
the graph of ![]() , this
looks right. Of course, that's not a very reliable way to go about
verifying the answer. The right thing to do is to substitute w
into the function ts and see what we get. It's possible to get
Maple to show that this is an exact solution but it takes several steps
and, after all, we're just verifying the result. It should be enough
just to get the floating-point value of the function at w:
, this
looks right. Of course, that's not a very reliable way to go about
verifying the answer. The right thing to do is to substitute w
into the function ts and see what we get. It's possible to get
Maple to show that this is an exact solution but it takes several steps
and, after all, we're just verifying the result. It should be enough
just to get the floating-point value of the function at w:
> evalf(ts(w));
![]()
For all intents and purposes, this is 1. The small difference is due to round-off error and is to be expected when doing finite-precision floating-point calculations.