Chemistry 3730 Fall 2000 Quiz 3 Solutions

1.

> phi := x -> exp(-beta*x^2);

$$\phi := x\rightarrow e^{( - \beta \,x^{2})}$$

> assume(beta>0);
> V := x -> Vmax*(1-exp(-alpha*x^2));

$$V := x\rightarrow \mathit{Vmax}\,(1 - e^{( - \alpha \,x^{2})})$$

> Vmax := 1e-20;

$$\mathit{Vmax} := .1\,10^{-19}$$

> alpha := 1e22;

$$\alpha := .1\,10^{23}$$

> m := 1e-26;

$$m := .1\,10^{-25}$$

> hbar := (6.626e-34)/(2*Pi);

$$\mathit{hbar} := .3313000000\,10^{-33}\,{\displaystyle \frac {1}{ \pi }}$$

As usual, we break up the variational energy into pieces:

> Kip := -hbar^2/(2*m)*int(phi(x)*diff(phi(x),x$2),
                           x=-infinity..infinity);

$$\mathit{Kip} := .2743992250\,10^{-41}\,{\displaystyle \frac { \sqrt{\beta \symbol{126}}\,\sqrt{2}}{\pi ^{(3/2)}}}$$

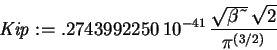
> Vip := int(phi(x)^2*V(x),x=-infinity..infinity);

$$\mathit{Vip} := .1253314137\,10^{-19}\,{\displaystyle \frac {... ...ol{126}}\,\sqrt{.5000000000 \,10^{22} + \beta \symbol{126}}}}$$

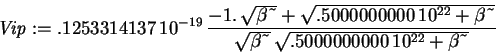
> ip := int(phi(x)^2,x=-infinity..infinity);

$$\mathit{ip} := {\displaystyle \frac {1}{2}} \,{\displaystyle \frac {\sqrt{2}\,\sqrt{\pi }}{\sqrt{\beta \symbol{126}}}}$$

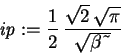
> Evar := (Kip+Vip)/ip;

$$\begin{eqnarray*}\lefteqn{\mathit{Evar} := ((.2743992250\,10^{-41}\, {\displayst... ...e height0.41em width0em depth0.41em} \right. \! \! \sqrt{\pi } \end{eqnarray*}$$

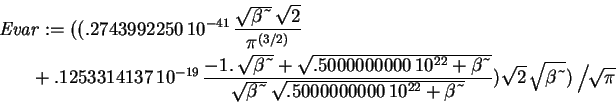
We now want to minimize this expression with respect to the variational parameter $\beta$:

> solve(diff(Evar,beta)=0,beta);

$$-.1073220371\,10^{23}, \,.3404729218\,10^{22}$$

The positive value is the only likely one. We can verify that it minimizes the variational energy by plotting this quantity for nearby values of $\beta$.

> plot(Evar,beta=1e21..5e21);

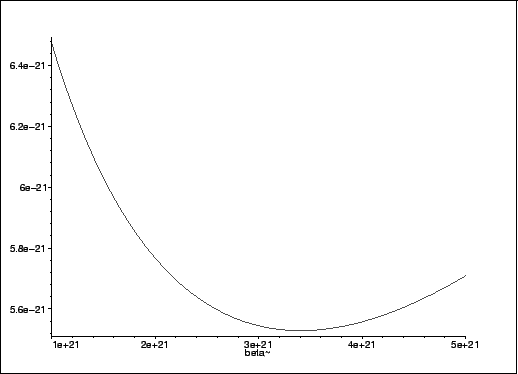
> assign(beta=.3404729218e22);
> evalf(Evar);

$$.5528474761\,10^{-20}$$

Thus, the variational energy is $5.53\times 10^{-21}\,\mathrm{J}$.

2.

I performed UHF calculations for both Li and Li⁺ using the 6-31G basis set. For Li, the highest occupied orbital has an energy of $-5.327\,\mathrm{eV}$ so that the ionization energy computed by Koopmans's theorem is 5.327eV. The ground state energies of Li and of Li⁺ are, respectively, -4663.171 and $-4520.332\,\mathrm{kcal/mol}$. The difference between these values is 122.839kcal/mol or 5.327eV. The experimental value is 5.392eV. Thus, the Koopmans theorem and difference values agree while they differ from the experimental value by 0.065eV.