Chemistry 3730 Fall 2000 Quiz 2 Solutions

1.

(a)

The potential energy term

> H1 := x -> V0*exp(-alpha^2*x^2);

$$\mathit{H1} := x\rightarrow \mathit{V0}\,e^{( - \alpha ^{2}\,x^{2 })}$$

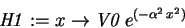
acts as a perturbation to the harmonic oscillator problem. We will therefore want to calculate energy corrections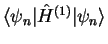 $\langle\psi_n\vert\hat{H}^{(1)}\vert\psi_n\rangle$. Let us start by defining the wavefunctions of the harmonic oscillator:

> A := n -> sqrt(beta/(2^n*n!*sqrt(Pi)));

$$A := n\rightarrow \sqrt{{\displaystyle \frac {\beta }{2^{n}\,n \mathrm{!}\,\sqrt{\pi }}} }$$

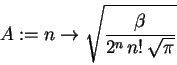
> with(orthopoly,H);

[H]

> psi0 := (n,x) -> A(n)*H(n,beta*x)*exp(-beta^2*x^2/2);

$$\psi 0 := (n, \,x)\rightarrow \mathrm{A}(n)\,\mathrm{H}(n, \, \beta \,x)\,e^{( - 1/2\,\beta ^{2}\,x^{2})}$$

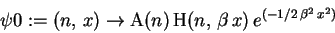
> assume(alpha>0);

> assume(beta>0);

The energy of the unperturbed oscillator is

> E0 := n -> hbar*omega0*(n+1/2);

$$\mathit{E0} := n\rightarrow \mathit{hbar}\,\omega 0\,(n + {\displaystyle \frac {1}{2}} )$$

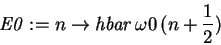
We now calculate the correction to the energy for n=0:

> int(psi0(0,x)*H1(x)*psi0(0,x),x=-infinity..infinity);

$${\displaystyle \frac {\beta \symbol{126}\,\mathit{V0}}{\sqrt{ \beta \symbol{126}^{2} + \alpha \symbol{126}^{2}}}}$$

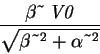
The energy of the perturbed system for n=0 is therefore

> E0(0) + %;

$${\displaystyle \frac {1}{2}} \,\mathit{hbar}\,\omega 0 + {\d... ...}}{\sqrt{ \beta \symbol{126}^{2} + \alpha \symbol{126}^{2}}}}$$

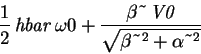
The calculation is exactly analogous for the next quantum level:

> int(psi0(1,x)*H1(x)*psi0(1,x),x=-infinity..infinity);

$${\displaystyle \frac {\beta \symbol{126}^{3}\,\mathit{V0}}{(\beta \symbol{126}^{2} + \alpha \symbol{126}^{2})^{(3/2)}}}$$

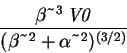
Total energy:

> E0(1)+%;

$${\displaystyle \frac {3}{2}} \,\mathit{hbar}\,\omega 0 + {\d... ...(\beta \symbol{126}^{2} + \alpha \symbol{126}^{2})^{(3/2)}}}$$

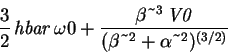
(b)

The perturbing potential has the following appearance:

> plot(subs(V0=5e-21,alpha=1e11,H1(x)),x=-3e-11..3e-11);

(The values of V₀ and of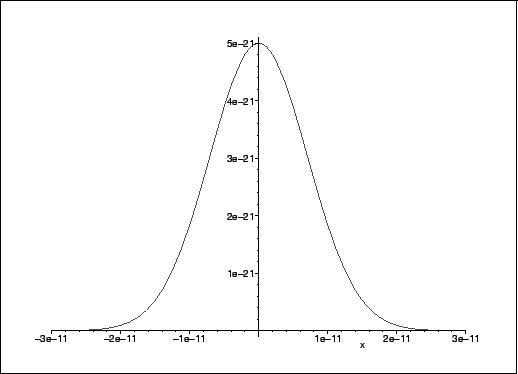 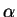$\alpha$ can be arbitrarily chosen. The values I used here correspond to values used below.) Since the perturbation is largest near x=0, we expect the probability density of the perturbed problem to be depressed in this region relative to the harmonic oscillator wavefunctions. Instead of sketching the wavefunctions, I am going to calculate them for particular values of the parameters.

> c := (n,k) ->
int(psi0(k,x)*H1(x)*psi0(n,x),x=-infinity..infinity)/(E0(n)-E0(k));

$$c := (n, \,k)\rightarrow {\displaystyle \frac {{\displaystyle... ...1}(x)\, \psi 0(n, \,x)\,dx}{\mathrm{E0}(n) - \mathrm{E0}(k)}}$$

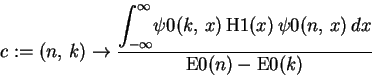
Note that since the perturbation is even, the coefficients will only be nonzero if both wavefunctions are either even or odd.

h := 6.6261e-34;

$$h := .66261\,10^{-33}$$

> hbar := h/(2*Pi);

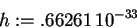
$$\mathit{hbar} := .3313050000\,10^{-33}\,{\displaystyle \frac {1}{ \pi }}$$

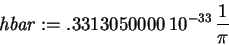
> k := 300;

k := 300

> m := 1e-26;

$$m := .1\,10^{-25}$$

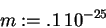
> beta := sqrt(sqrt(k*m)/hbar);

$$\beta := .7230466506\,10^{11}\,\sqrt{\pi }$$

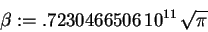
> omega0 := sqrt(k/m);

$$\omega 0 := .1732050808\,10^{15}$$

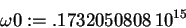
> V0 := 5e-21;

$$\mathit{V0} := .5\,10^{-20}$$

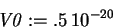
> alpha:=1e11;

$$\alpha := .1\,10^{12}$$

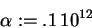
> evalf(c(0,2));

.02887528958

> evalf(c(0,4));

-.004731798083

The first correction term is much larger than all the others. It is probably best just to stop at this term. The normalization factor can be shown to be

> N0 := 1/sqrt(1 + c(0,2)^2);

$$\mathit{N0} := {\displaystyle \frac {1}{\sqrt{1 + .00008447981444 \,\pi ^{2}}}}$$

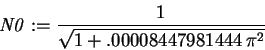
so that the normalized wavefunction is

> psi_0 := x -> N0*(psi0(0,x)+c(0,2)*psi0(2,x));

$$\mathit{psi\_0} := x\rightarrow \mathit{N0}\,(\psi 0(0, \,x) + \mathrm{c}(0, \,2)\,\psi 0(2, \,x))$$

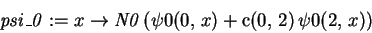
Let us now plot the probability density corresponding to this wavefunction in relation to the harmonic oscillator density:

> plot([psi0(0,x)^2,psi_0(x)^2],x=-3e-11..3e-11,
       color=[red,blue],axes=FRAME);

Note that, as we predicted, the perturbed wavefunction is smaller near x=0, where the perturbation is largest.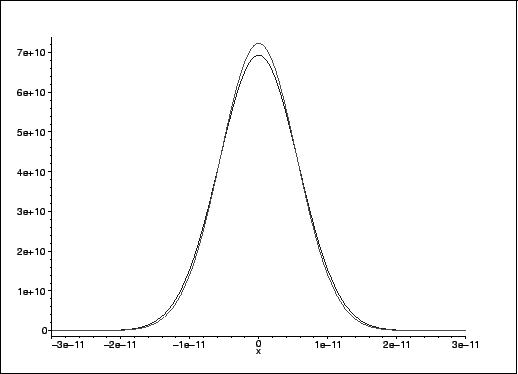

Now for n=1:

> evalf(c(1,3));

.03108627633

> evalf(c(1,5));

-.006576471357

Again, it is probably best just to keep the first term.

> N1 := 1/(sqrt(1+c(1,3)^2));

$$\mathit{N1} := {\displaystyle \frac {1}{\sqrt{1 + .00009791239206 \,\pi ^{2}}}}$$

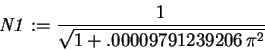
> psi_1 := x -> N1*(psi0(1,x)+c(1,3)*psi0(3,x));

$$\mathit{psi\_1} := x\rightarrow \mathit{N1}\,(\psi 0(1, \,x) + \mathrm{c}(1, \,3)\,\psi 0(3, \,x))$$

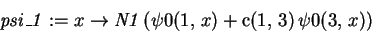
plot([psi0(1,x)^2,psi_1(x)^2],x=-3e-11..3e-11,color=[red,blue]);

Again, the probability density is somewhat depressed near x=0and enhanced further away.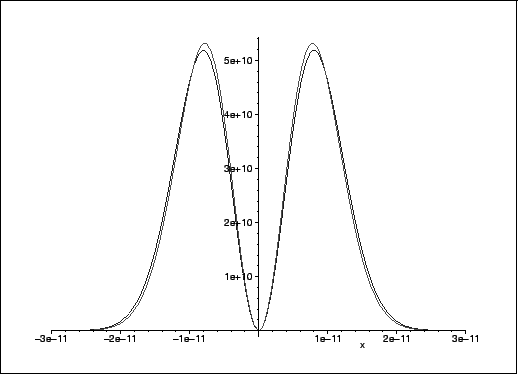

2.

The two quantities given are compatible if the commutator of their operators is zero.

$$\begin{eqnarray*}% latex2html id marker 169 [\hat{x},\hat{p}_x^2-\hbar\hat{p}_x]... ...\hbar\right) \not= 0\\ \therefore & & \textrm{not compatible} \end{eqnarray*}$$