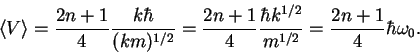Chemistry 3730 Fall 2000 Quiz 1 Solutions

1.

We start by defining the particle-in-a-box wavefunction:

> psi_pib := (n,x,L) -> sqrt(2/L)*sin(n*Pi*x/L);

$$\mathit{psi\_pib} := (n, \,x, \,L)\rightarrow \sqrt{2\, {\dis... ...}{L}} }\,\mathrm{sin}({\displaystyle \frac {n\,\pi \,x}{L}} )$$

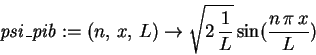
Computing probabilities is then a straightforward matter:

> evalf(int(psi_pib(1,x,L)^2,x=0..L/4));

.09084505693

> evalf(int(psi_pib(2,x,L)^2,x=0..L/4));

.2500000000

> evalf(int(psi_pib(3,x,L)^2,x=0..L/4));

.3030516477

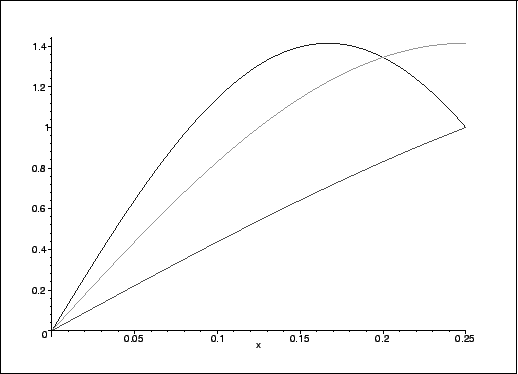
To understand why these values are as they are, we consider the shapes of the wavefunctions. It is useful to focus on the leftmost quarter for which we computed occupation probabilities:

> plot([psi_pib(1,x,1),psi_pib(2,x,1),psi_pib(3,x,1)],
  x=0..1/4,color=[red,green,blue]);

The n=1 wavefunction peaks in the centre of the box so the probability density is small at the edges of the box. The n=2 wavefunction has a simple two-fold antisymmetry, each lobe itself having a simple reflection symmetry about its centre so that exactly one quarter of the probability density can be found in each of the quarters of the box. For n=3, the probability density is divided into three similar lobes. The leftmost quarter of the box contains one of the probability density maxima, so the probability of finding the particle in this region is elevated.

2.

Again, we start by defining the wavefunction. We can do it in pieces to simplify our typing.

A := n -> sqrt(beta/(2^n*n!*sqrt(Pi)));

$$A := n\rightarrow \sqrt{{\displaystyle \frac {\beta }{2^{n}\,n \mathrm{!}\,\sqrt{\pi }}} }$$

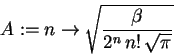
> with(orthopoly,H);

[H]

> psi := (n,x) -> A(n)*H(n,beta*x)*exp(-beta^2*x^2/2);

$$\psi := (n, \,x)\rightarrow \mathrm{A}(n)\,\mathrm{H}(n, \,\beta \,x)\,e^{( - 1/2\,\beta ^{2}\,x^{2})}$$

> assume(beta>0);

We now proceed to compute the expectation values:

> int(psi(0,x)*1/2*k*x^2*psi(0,x),x=-infinity..infinity);

$${\displaystyle \frac {1}{4}} \,{\displaystyle \frac {k}{\beta \symbol{126}^{2}}}$$

> int(psi(1,x)*1/2*k*x^2*psi(1,x),x=-infinity..infinity);

$${\displaystyle \frac {3}{4}} \,{\displaystyle \frac {k}{\beta \symbol{126}^{2}}}$$

> int(psi(2,x)*1/2*k*x^2*psi(2,x),x=-infinity..infinity);

$${\displaystyle \frac {5}{4}} \,{\displaystyle \frac {k}{\beta \symbol{126}^{2}}}$$

The pattern is reasonably obvious:

$$\langle V\rangle = \frac{2n+1}{4}\frac{k}{\beta^2}.$$

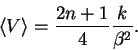
Now we use the definition of $\beta$:

$$\langle V\rangle = \frac{2n+1}{4}\frac{k\hbar}{(km)^{1/2}} =... ...{4}\frac{\hbar k^{1/2}}{m^{1/2}} = \frac{2n+1}{4}\hbar\omega_0.$$