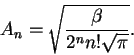Up: Back to the Chemistry 3730 test index
Chemistry 3730 Fall 2000 Quiz 1
Name:
For each question, write out the expressions which you need to evaluate
in standard mathematical notation. Note that information required for
the solution of these problems is given on the reverse of this page.
- 1.
- Calculate the probability that a particle in a box is to be
found in the leftmost quarter (
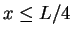 )
of the box for n=1,
2 and 3. Give your answers to 4 significant figures. Compare the
relative values of your answers and relate them to the shapes of
the wavefunctions. [10 marks]
)
of the box for n=1,
2 and 3. Give your answers to 4 significant figures. Compare the
relative values of your answers and relate them to the shapes of
the wavefunctions. [10 marks]
Maple hint: 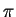 is typed `Pi' in Maple.
is typed `Pi' in Maple.
- 2.
- Calculate the average potential energy for a harmonic oscillator
for n=0, 1 and 2. Give your answers in terms of
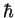 and
and
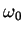 .
Can you discern a pattern in your answers?
[10 marks]
.
Can you discern a pattern in your answers?
[10 marks]
Maple hints: To use the Hermite polynomials, type
with(orthopoly,H);
In Maple, Hn(u) is typed H(n,u)
and eu is exp(u).
It is best to do
all the calculations in terms of 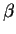 and to simplify by hand
at the end. It will be necessary to inform Maple that
and to simplify by hand
at the end. It will be necessary to inform Maple that 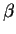 is a positive parameter.
is a positive parameter.
The particle-in-a-box wavefunctions are of the form
The harmonic oscillator potential energy is
and the wavefunctions are of the form
where Hn(u) is a Hermite polynomial and
Additionally,
and



Up: Back to the Chemistry 3730 test index
Marc Roussel
2000-10-16
![]() is typed `Pi' in Maple.
is typed `Pi' in Maple.
![]() is typed `Pi' in Maple.
is typed `Pi' in Maple.