Chemistry 3730 Fall 2000 Assignment 4 Solutions

1.

The variational wavefunction is

> phi := r -> exp(-alpha*r^2);

$$\phi := r\rightarrow e^{( - \alpha \,r^{2})}$$

> assume(alpha>0);

We break up the variational energy into three pieces, as usual:

> Kip := -hbar^2/(2*mu)*int(int(int(phi(r)*diff(r^2*diff(phi(r),r),r)
         *sin(theta),r=0..infinity),theta=0..Pi),phi=0..2*Pi);

$$\mathit{Kip} := {\displaystyle \frac {3}{8}} \,{\displaystyle... ...\,\pi ^{(3/2)}\,\sqrt{2}}{\mu \,\sqrt{ \alpha \symbol{126}}}}$$

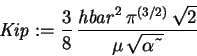
> Vip := -Z*e^2/(4*Pi*epsilon0)*int(int(int(phi(r)^2*r*sin(theta),
         r=0..infinity),theta=0..Pi),phi=0..2*Pi);

$$\mathit{Vip} := - {\displaystyle \frac {1}{4}} \,{\displaystyle \frac {Z\,e^{2}}{\varepsilon 0\,\alpha \symbol{126}}}$$

> ip := int(int(int(phi(r)^2*r^2*sin(theta),r=0..infinity),
        theta=0..Pi),phi=0..2*Pi);

$$\mathit{ip} := {\displaystyle \frac {1}{4}} \,{\displaystyle \frac {\pi ^{(3/2)}\,\sqrt{2}}{\alpha \symbol{126}^{(3/2)}}}$$

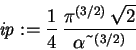
> Evar := (Kip+Vip)/ip;

$$\mathit{Evar} := 2\,{\displaystyle \frac {({\displaystyle \fr... ...}}} )\,\alpha \symbol{126}^{(3/2)}\,\sqrt{2}}{ \pi ^{(3/2)}}}$$

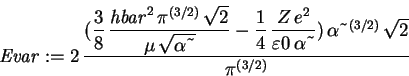
We minimize the variational energy with respect to the variational parameter $\alpha$:

> solve(diff(Evar,alpha)=0,alpha);

$${\displaystyle \frac {1}{18}} \,{\displaystyle \frac {Z^{2}\,... ...}\,\mu ^{2}}{\pi ^{3}\,\mathit{hbar}^{4}\,\varepsilon 0^{2}}}$$

> assign(alpha=1/18*Z^2*e^4*mu^2/(Pi^3*hbar^4*epsilon0^2));

We can now evaluate the variational energy:

> simplify(Evar);

$$- {\displaystyle \frac {1}{12}} \,{\displaystyle \frac {( - Z... ...\,Z\,e^{2}}{\pi ^{3}\,\mathit{hbar}^{2}\, \varepsilon 0^{2}}}$$

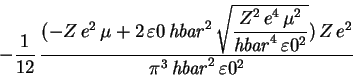
> assume(Z>0);
> assume(e>0);
> assume(mu>0);
> assume(hbar>0);
> assume(epsilon0>0);
> simplify(%);

$$- {\displaystyle \frac {1}{12}} \,{\displaystyle \frac {\math... ...athit{hbar\symbol{126}}^{2}\,\varepsilon 0 \symbol{126}^{2}}}$$

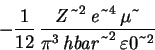
Now to compute the percent error:

> Eexact := -Z^2*e^4*mu/(32*Pi^2*epsilon0^2*hbar^2);

$$\mathit{Eexact} := - {\displaystyle \frac {1}{32}} \, {\displ... ...arepsilon 0 \symbol{126}^{2}\,\mathit{hbar\symbol{126}}^{2}}}$$

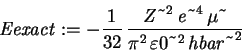
> simplify((Eexact-Evar)/Eexact);

$${\displaystyle \frac {1}{3}} \,{\displaystyle \frac { - 8 + 3\, \pi }{\pi }}$$

> evalf(%);

.1511736370

Thus, the error in the Gaussian approximation is about 15%.

2.

(a)

Very similar results are obtained with the 6-311G and D95^* basis sets. However, the former basis set uses 13 basis functions while the latter uses 16. Accordingly, the 6-311G basis set is the better one to use. With this basis set we find a ground-state energy of $-9144.0\,\mathrm{kcal/mol}$.

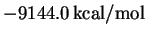(b)

Adding extra basis functions doesn't reduce the energy much in this case. This suggests that the 6-311G basis set is large enough to reach the Hartree-Fock limit for beryllium.

3.

(a)

I expect Fe³⁺ to have a half-filled 3d subshell so the spin multiplicity I used was 6. I performed an STO-6G^* calculation, adding an spd shell with an orbital exponent of 21. The computed energy was $-789\,905.1\,\mathrm{kcal/mol}$.

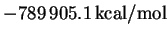(b)

The computed electronic configuration is

1s²2s²2p⁶3s²3p⁶3d⁵.

This agrees with what we would have predicted based on the usual rules.