- 1.
- Suppose that a particle is confined to a two-dimensional square box,
i.e. one for which Lx=Ly=L. It is easy to find different sets of
quantum numbers which give the same energy. For instance, we get
the same energy if nx=1 and ny=2 as we do if nx=2 and
ny=1. Of course, this is a trivial sort of degeneracy.
However, there are more interesting degeneracies in which the
two sets of quantum numbers are not just permutations of each
other. Find one. [5 marks]
Hints: Maple has a function called isolve() which finds
integer solutions to equations. Its syntax is similar to that of
solve(). There will be a certain amount of trial and
error involved in solving this problem. The idea is to set up
an equation which will have two or more significantly different
and physically significant (i.e. with quantum numbers that make
sense for a particle in a box) solutions when the energy is
degenerate.
- 2.
- Calculate the expected value of the kinetic energy for the
harmonic oscillator for n=0, 1 and 2. Can you detect a pattern
in your answers? Relate the average kinetic energy to the total
energy of the oscillator. [10 marks]
Hints: Maple will need to know that 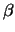 is positive.
Once you have computed the average kinetic energies and picked
up the pattern, use the definitions
is positive.
Once you have computed the average kinetic energies and picked
up the pattern, use the definitions
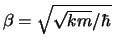 and
and
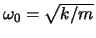 to relate the
kinetic and total energies. This is easiest to do by hand.
to relate the
kinetic and total energies. This is easiest to do by hand.
- 3.
- Show that the harmonic oscillator with n=0 obeys the uncertainty
principle. [10 marks]
Maple hint: Maple will need to know that 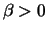 and that
and that 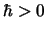 .
.
- 4.
- Work out (by hand is easiest) the coordinates of the classical
turning points for the harmonic oscillator as a function of the
quantum number n and of the parameter
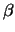 .
Write a function which returns the probability that the particle
is to be found outside of the classical turning points. Then
plot your function starting at n=0 and going up to some
reasonably large value of the quantum number. What happens to
this probability at large n? [15 marks]
.
Write a function which returns the probability that the particle
is to be found outside of the classical turning points. Then
plot your function starting at n=0 and going up to some
reasonably large value of the quantum number. What happens to
this probability at large n? [15 marks]
Hints and notes:
The ability to compute Hermite polynomials must be loaded into
Maple by the command
with(orthopoly,H);
Make sure that 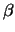 is undefined before you start this
problem.
Maple will need to know that
is undefined before you start this
problem.
Maple will need to know that 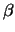 is positive. When writing
the function that computes the probability, use the fact that
the probability that the particle is outside
the classical turning points is twice the probability that it is
(for instance) to the right of the positive turning point.
Furthermore, you will have to use
is positive. When writing
the function that computes the probability, use the fact that
the probability that the particle is outside
the classical turning points is twice the probability that it is
(for instance) to the right of the positive turning point.
Furthermore, you will have to use simplify() in your
function to get Maple to cancel out the 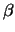 's after
performing the integral.
The calculations are a little CPU intensive so start by plotting
a limited range of values, extending the range a little at a
time until you run out of patience.
's after
performing the integral.
The calculations are a little CPU intensive so start by plotting
a limited range of values, extending the range a little at a
time until you run out of patience.
![]() is positive.
Once you have computed the average kinetic energies and picked
up the pattern, use the definitions
is positive.
Once you have computed the average kinetic energies and picked
up the pattern, use the definitions
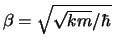 and
and
![]() to relate the
kinetic and total energies. This is easiest to do by hand.
to relate the
kinetic and total energies. This is easiest to do by hand.
![]() and that
and that ![]() .
.