5:40 am Edmonton, Alberta
I purchased 6 books at the University of Alberta Bookstore yesterday. Three of these were on mathematics and one was on Learning:
- The Calculus Tutoring Book (1986) Carol Ash & Robert B. Ash.
- The Adventure of Numbers (2004) Gilles Godefroy
- The Mathematics of Oz (2002) Clifford Pickover
- Content Area Reading (2005) Richard & Jo Anne Vacca, Deborah Begoray
The first looks like a promising supplement to my other books on calculus. I must return to this topic! It should be scheduled for alternate days. The Godefrey book appears as a classic description of the evolution of the concepts that deal with the various ideas about numbers. Pickover's book is another of his delightful compediums of recreational mathematics. These are an important component of Learning math - where the emphasis is on divergent thinking, problem solving in the true sense of the word, and having fun. I must remind myself to collect together both Pickover's books as well as many I have by Martin Gardner.
Thus my topics are now:
- Calculus
- Number Theory
- Recreational Mathematics
This feels right to me: a nice balance between formalism and fun.
Now to rearrange the following table to incorporate these books.
| Mathematics |
|
|
|
| Description |
Start |
End |
Done |
| Calculus |
| Calculus (1994) Michael Spivak |
|
|
|
| |
|
|
|
| What is Mathematics? (1941) Richard Courant & Herbert Robbins |
|
|
|
| |
|
|
|
| The Calculus Tutoring Book (1986) Carol & Robert Ash |
|
|
|
| |
|
|
|
| Number Theory |
What is Mathematics? (1941) Richard Courant & Herbert Robbins |
|
|
|
Read chap 1 The natural numbers [p. 1 - 20] |
Sept 26 |
Sept 29 |
Yes |
Notes for chap 1.1 Calculation with integers [p. 1 - 9] |
Sept 26 |
Sept 26 |
Yes |
Notes for chap 1.2 The infinitude of the number system [p. 9 - 20] |
Sept 26 |
Sept 26 |
Yes |
| Read chap 1 supplement The theory of numbers [p. 21 - 51] |
Sept 29 |
|
|
| Notes for chap 1 supplement 1.1 The prime numbers [p. 21 - 31] |
Sept 29 |
Oct 01 |
Yes |
| Notes for chap 1 supplement 1.2 Congruences [p. 31 - 40] |
Oct 03 |
|
|
| Notes for chap 1 supplement 1.3 Pythagorean numbers and Fermat's Last Theorem [p. 40 - 42] |
Oct 04 |
|
|
| Notes for chap 1 supplement 1.4 The Euclidean Algorithm [p. 42 - 51] |
|
|
|
| |
|
|
|
| Calculus (1994) Michael Spivak |
|
|
|
| Read chap 1 Basic properties of numbers [p. 3 - 20] |
|
|
|
| Notes for chap 1 |
|
|
|
| Exercises for chap 1 [p. 13 - 20] |
|
|
|
| |
|
|
|
| In Code (2001) Sarah Flannery |
|
|
|
| Part I Background [p. 1 - 40] |
Oct 07 |
Oct 08 |
Yes |
| Part II Mathematical Excursions [p. 41 - 186] |
Oct 08 |
|
|
| |
|
|
|
| Prime Obsession (2003) John Derbyshire |
|
|
|
Reread chap 1 - 8 [p. 1 - 136] |
|
|
|
| |
|
|
|
| The Adventure of Numbers (2004) Gilles Godefroy |
|
|
|
| |
|
|
|
| Recreational Mathematics |
| The Mathematics of Oz (2002) Clifford Pickover |
|
|
|
| |
|
|
|
Review
I reread the first 90 pages of Sarah Flannery's book, "In Code". It is a nice blend of autobiography and mathematics, a bit like this web site. Now to make a few notes on the first part (chapters 1 - 3)
|
| Here are a few quotes from "In Code" that I enjoyed: |
Quotation |
Comment |
| "Ever since I can remember, my father has given us little problems and puzzles. ... These problems challenged us and encouraged our curiousity ... they taught us how to reason and think for ourselves. [p. 8] |
This reinforces my decision to buy the Pickover book, and to set aside a few others that I have purchased over the years.
I am now going to set aside specific times where I play with these (1/3 calculus, 1/3 number theory, and 1/3 recreational math).
Such puzzles, which may require time to explore, should also occupy 1/3 of the school curriculum. |
| "This variation on a theme lets you learn the very valuable lesson that sometimes problems may not have solutions of the type you seek." [p. 10] |
The idea that some problems may not have a solution is one that needs reminding. |
| "Once you see and solve (or just hear the solution to) a problem of this type, you learn to be careful and to watch out for little wrinkles." [p. 12] |
Another useful reminder. |
| "When you finally crack a problem, whether by yourself or with some help, you experience a great feeling of self-satisfaction and pride." [p. 13] |
I agree, yet I wonder how many people have experienced this feeling. |
| "For years I had the advantage ... of hearing mathematics spoken in a natural way between my father and a physicist friend of his in our kitchen. ... I realized with some relief that the people I supposed could solve every math problem were, in fact, often struggling." [p. 31] |
I recall a similar event when I was an undergraduate and asked a professor for help on a statistics problem that was outside of our regular work. |
| "But those projects were really no more than gathering and marshalling information in an attractive way (in fact, organizing - which I love; I'm not quite good as keeping organized, though ...) [p. 33] |
Two points:
1) many activities are superficial and require little or no original thought,
2) organizing is a major theme in this web site, and keeping organized is a challenge. |
| " 'It'll take time to assimilate the concepts, to let them mature and become clear in your mind. Anyway, you are almost sure to run into all sorts of difficulties at the programming end when you try to implement the mathematics. Projects don't have to be hectic affairs; better if you give yourself plenty of time and that you take your time.' " [p. 36] |
Once again, this applies to this web site, and to my goal of Learning calculus.
But I am very comfortable with the time scale. This may take a few years, but they will be enjoyable years with a "great feeling of self-satisfaction". |
| "He often advises, 'Speak clearly and simply. Tell a person what you know and come clean when you don't know something. Don't bluff.' " [p. 37] |
This has been my mantra since I first worked as a computer programmer in Montreal in the 1960's. |
| "The project required that I learn number theory (really learn it), the necessary cryptographic ideas and how to program in Mathematica so I could implement and illustrate the cryptographic schemes." [p. 38] |
Three points:
1) there is a huge distinction between learning and "really learning". Really learning must be self-imposed.
2) I have yet to tackle programming in Mathematica. It is time to have a look at this!
3) The idea of simulating a situation in Mathematica is one that I should begin to play with. In my own words, "If you think you really understand something, try building a model to represent your understanding." |
| "One of Dad's favorite books, Excursions in Calculus by Robert M. Young." [p. 44] |
I have checked this at amazon.ca and it is available but 4 -6 week delay. It is not available at chapters.ca. There is not much information on it, |
| "I would come to appreciate that it wasn't good enough to know any old way of doing something - you had to find methods or techniques that implement the theory in highly efficient ways." [p. 59] |
This is in contrast with the view of many mathematicians, who remain in the realm of the abstract. |
| |
|
The book is full of useful asides. |
Content
In Code (2001) by Sarah Flannery
Hilbert numbers: 4n + 1
- closed under multiplication
- Hilbert prime: no other Hilbert numbers as factors
- Prime factorization is not unique.
- this does not appear to be mainstream mathematics
Fermat numbers: 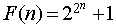
Euler numbers: 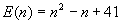
- the first 40 values of n yield prime numbers
Mersenne numbers: 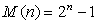
|
Description |
Start |
End |
Quality |
| Number Theory (Courant & Robbins) |
Sept 30 |
Sept 30 |
1 |
Prime Numbers |
Sept 30 |
Sept 30 |
1 |
Algebraic relationships
|
Sept 30 |
Sept 30 |
3 |
Distribution of prime numbers
|
Sept 30 |
Sept 30 |
3 |
The Prime Number Theorem
|
Sept 30 |
Sept 30 |
3 |
Congruences |
Sept 30 |
Sept 30 |
1 |
Geometric representation
|
Sept 30 |
Sept 30 |
3 |
Rules for divisibility
|
Sept 30 |
Oct 03 |
2 |
Fermat's Theorem
|
Oct 03 |
Oct 04 |
2 |
Quadratic residues
|
Oct 04 |
|
|
Pythagorean Numbers |
|
|
|
Fermat's Last Theorem
|
|
|
|
Division |
|
|
|
Euclidean algorithm
|
|
|
|
Diophantine equations
|
|
|
|
Euler's phi function
|
|
|
|
| |
|
|
|
The next chapter in "In Code" is called The Arithmetic of Cryptography [p. 71 - 112]. That, and the following chapter, Sums With a Difference provide the detail of the mathematics underlying cryptography. Now to do some slow reading, some yellow highlighting, and some hand written notes. This has been a good morning.
8:00 am Total elapsed time for the day: 2 hr. 20 min |