Read chap 1 The natural numbers [p. 1 - 20]

Notes for chap 1.1 Calculation with integers [p. 1 - 9]

Notes for chap 1.2 The infinitude of the number system [p. 9 - 20]

Review

I am still playing with Section 1.2 of Courant & Robbins on The Infinitude of the Natural Number System. I have a deep appreciation of the idea of an infinite series and a sense that some series sum to a relatively simple algebraic expression. This expression may give a clear sense of what happens when the series is extended forever. I recall from undergraduate days that some series diverge and some converge, but I do not recall any specific details on how to determine this. Spivak discusses this topic near the end of his Calculus text, so I will take that as a signal that I can defer the topic until later.

This will lead to a few special formulas as well as the binomial theorem and Pascal's triangle.

Content

Here are two special formulas for a finite series of squares and cubes of integers.

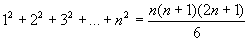
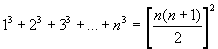
It is a straight forward application of algebra to prove both of these formalas by mathematical induction. Clearly both series are infinitely large as n increases without bound. The fun begins when the terms get smaller as n increases. Then anything is possible.

Courant & Robbins then introduce the inequality

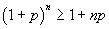
which holds for all p>-1 and all positive integers n.

This may also be proven by mathematical induction, the key idea being that the expansion of the left side will contain the right hand side plus some additional terms.

Apparently this inequality will be useful in subsequent work. This is where faith comes in.

Faith continues when they claim that it is often useful to know the explicit expression for the expansion of .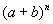

The expansion of 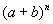is called the binomial theorem and is a classic case of complex notation. The notation is complex because the formula is complex. Here are two different ways of expressing this expansion.

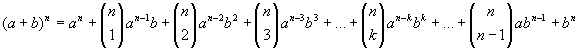
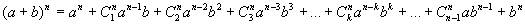
where .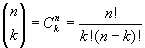

This completes my notes for chapter 1.2 [p. 9 - 20]

Courant & Robbins then have a Supplement to Chapter 1 "The Theory of Numbers" [p. 21 - 51] which discusses:

• The Prime Numbers
• Congruences (number bases)
  • General concepts
  • Fermat's Theorem
  • Quadratic Residues
• Pythagorean Numbers & Fermat's Last Theorem
• The Euclidean Algorithm
  • General Theory
  • Application to the Fundamental Theorem of Arithmetic
  • Euler's f Function. Fermat's Theorem Again
• Continued Fractions. Diophantine Equations

Fascinating! I know the concept of a prime number and have begun to realize that Riemann is associated with the distribution of the primes. I recall from a few days ago that the natural logarithmic function is related to this but this is not yet automatic for me. I also can recall the basic idea of number bases but am not familiar with the terminology of congruences (except for the term modula, which is a synonym for base). I believe that the fundamental theorem of arithmetic is that every number has a unique prime factorization. I recognize the phrase Diophantine equations but really have no idea what the phrase refers to. This promises to be an interesting chapter with the reward at the end being that I will then have a good understanding of the above topics. This appears to be a good introduction to number theory. Following this I should be able to return to Derbyshire's book "Prime Obsession". And perhaps I will then be motivated to search for a good reference book on number theory. While returning to my goal of understanding calculus, which first requires a strong review of the concepts of function and limit.