5:30 am Lethbridge, Alberta
After getting diverted to a couple of worthwhile activities (mathematics timeline, schematic chart of chapters 1, 3 & 5) yesterday morning, I am determined to make my notes for chapters 5 & 6 this morning.
Review
I have begun reading "Prime Obsession" by John Derbyshire. I hope to stay with this book until the end and then return to Michael Spivak's "Calculus". |
| My next step will be to make a few notes about chapters 5 & 6 [p. 63 - 98]. |
Content
Prime Obsession. Chapter 5 Riemann's Zeta Function [p. 63 - 81]
In 1689 mathematicians began to think about the series
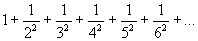
This series is similar to the harmonic series, except that each term is the square of the corresponding term of the harmonic series. Recall that the harmonic series diverges. In this case each term is much smaller than the corresponding term of the harmonic series. Does this series converge, and if so to what value? 46 years later, in 1735, Leonhard Euler showed that the series does converge to a value of 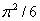 .This problem opened the door to the zeta function, which is the mathematical object of the Riemann hypothesis. .This problem opened the door to the zeta function, which is the mathematical object of the Riemann hypothesis.
Some more background. The idea of an exponent began as a way of expressing repeated multiplication. That is, 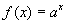 . What happens if we extend the idea of the exponent as being any number, not just a positive integer. Now the idea of exponent is no longer repeated addition but is the extension of the the basic power rules for positive integers to the cases where the exponent is any number. . What happens if we extend the idea of the exponent as being any number, not just a positive integer. Now the idea of exponent is no longer repeated addition but is the extension of the the basic power rules for positive integers to the cases where the exponent is any number.
Still more background. Now that I have functions of the form 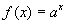 , what is the corresponding inverse function? (Recall that mathematicians like to have an inverse for any function.) This is the logarithm of x to the base a. , what is the corresponding inverse function? (Recall that mathematicians like to have an inverse for any function.) This is the logarithm of x to the base a.
One should play around with both exponents and logarithms until one is quite familiar with them, particularly the natural logs and the number e. I will do that in another session using Mathematica.
It turns out that the logarithm of x increases very slowly. The natural logarithm of x increases slower than any power of x, where the power of x can be very small. Further, any power of log x eventually increases more slowly than any power of x. Said differently:
The graph of 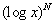 will eventually drop below, and for ever stay below, the graph of will eventually drop below, and for ever stay below, the graph of 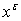 , no matter how big N is or how small e is. , no matter how big N is or how small e is.
Euler actually showed that the series 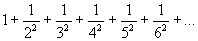 converges for any even integer exponent. However if the exponent was an odd integer, he was unable to make a definitive statement. converges for any even integer exponent. However if the exponent was an odd integer, he was unable to make a definitive statement.
Riemann defined the zeta function as the generalized function of this power series:
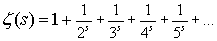
Then, when s is 1 we have the familiar harmonic series and it diverges. When s is an even positive integer, Euler showed that the function converges to a value involving the number p.
This chapter has been involved with the properties of infinite series, and in particular of a family of functions that are now known as the zeta function.
Prime Obsession. Chapter 6 The Great Fusion. [p. 82 - 98]
See the following quotes for this chapter.
|
| Here are a few quotes from "Prime Obsession" that I enjoyed: |
Quotation |
Comment |
| "... they know from experience that getting that exact value often opens doors and throws light on the underlying math." [p. 64] |
|
| "This distinction between numbers for counting and numbers for measuring reaches deep into human habits of thought and speech. It is as if with one part of our minds we perceive the world as made up of distinct, solid objects that can be tallied; while with another, we see it as a collection of fabrics, grains, or fluids, to be divided up and measured. Keeping the two notions straight does not come easily." [p. 83] |
|
| "Our perceptions of the world are mirrored in our languages." [p. 83] |
This is very important. Somehow, in a symbiotic evolution of language and mind, the two have evolved and have led to both mathematics and science. |
| "The English language takes the world to be mainly a countable place: one cow, two fishes, three mountains, ..." [p. 83] |
|
| "The Chinese language, by contrast with English, takes very nearly the whole of creation to be measurable. One of the minor chores of learning Chinese is memorizing the right 'measure word' for each noun. ... In the entire Chinese language there are only two words that can always be let loose grammatically without a measure word: 'day' and 'year'. Everything else - cows, fishes, mountains, doors, stars - is a kind of stuff that must be divided up and measured out before we can talk about it." [p. 84] |
|
| "The much/many confusion has occasioned much argument and many inconveniences." [p. 84] |
|
| "At the opening of the nineteenth century the most fundamental concept of analysis, the concept of a limit, was not clearly understood even by the best minds." [p. 87] |
|
| "The concepts that analysis deals with - 'the infinite and the infinitesimal,' as Euler would have said; 'limits and continuity,' his modern counterpart would insist - are among the most difficult for the human mind to grasp." [p. 88] |
|
| "Mathematical thinking is, at some level, deeply unnatural. It goes against all the grain of human thought and language. ... A whale is, by any standard of complexity that makes sense, a vastly more complicated thing than 'five', yet it is much easier for the human mind to apprehend. Any tribe of human beings that was acquainted with whales would certainly have a word for them in their language; yet their are peoples whose language has no word for 'five' even though five-ness is there, quite literally, at their fingertips." [p. 89] |
But a whale is a concrete object, whereas 'five' is an abstract idea independent of the object. Thus the issue is one of the ease and value of direct perception (very useful for survival) and abstract thought (useful for economics and math and science and technology and philosophy and religion). We evolved for a few hundred thousand years before attaining the result of civilization, and we have only had a few thousand years to evolve within such a setting. It is amazing how quickly our abilities for abstraction have developed given how little practice we have had. |
| "The great fusion between arithmetic and analysis - between counting and measuring ... came about as the result of an inquiry into prime numbers, conducted by Lejeune Dirichlet in the 1830s." [p. 91] |
|
| "Inspired by a result Euler had proved precisely 100 years before, a result I hereby name 'the Golden Key', Dirichlet in 1837 brought together ideas from analysis and arithmetic to prove an important theorem about prime numbers. ... each unlimited arithmetic progression, whose first member and difference are whole numbers without common factor, contains infinitely many prime numbers." [p. 95] |
|
Riemann's zeta function is a generalized infinite series that will turn out to have important consequences for studying the distribution of prime numbers. I also am not yet sure about the ideas underlying Dirichlet's contribution. |
Before continuing the book, I want to spend a session or two with Mathematica and play with exponents and logarithms and their graphs. I also want to see what I can do with the zeta function in Mathematica.
7:30
am
Total elapsed time: 2 hr.
Total elapsed time for the day: 2 hr.
|