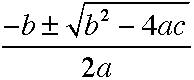|
Mathematics 15
October 28
|
|
Mathematics Chronology |
9:20 am
I skim-read chapter 7 Quadratic Reciprocity from "Fearless Symmetry" this morning and then switched to "The Equation that Couldn't be Solved" where I read the best biography of Galois that I have seen (chapter 5 The Romantic Mathematician [p. 112 - 157]. Meticulous detail. I followed this with a brief glance at the next chapter, called simply "Groups". It appears to be a clear description of the essential nature of group theory, showing the connections to permutations and to symmetry. Both this chapter and the Quadratic Reciprocity chapter involve some actual mathematics and thus require (me) to slow down and make sure that I understand what is being said.
The "Fearless Symmetry" book uses the mathematical concept of Representations as its cornerstone idea. "The Equation that Couldn't be Solved" focuses on the general problem of the solution of algebraic equations as the historical genesis of group theory. Both books emphasize the importance of the young French mathematician Everiste Galois, of group theory, and of symmetry.
A "representation" in mathematics is simply a function or mapping of a set of elements to another standard set that reveals some essential feature of the original set. I think I now have that idea.
|
Fearless Symmetry Chapter 6 Equations and Varieties [p. 49 - 66] (Review notes)
- Z is the set of integers.
- A Z-equation is an equality of polynomials with integer coefficients.
- A variety S defined by a Z-equation is the function that assigns to the number system A the set of solutions S(A).
It is important to realize that a variety refers to a particular set of Z-equations and then restricts the solution to a set of elements in a "number system" such as Z, Q, R, C,  . . |
Fearless Symmetry Chapter 7 Quadratic Reciprocity [p. 67 - 83]
- "Quadratic reciprocity was the first of all reciprocity laws, and it is closely connected with the theory of Galois representations." [p. 67]
- "Quadratic reciprocity is part of 'classical' number theory going back to the eighteenth century. It inspired the many other reciprocity laws that eventually developed into a large part of number theory." [p. 67]
| At this point I do not know what a reciprocity law is, let alone quadratic reciprocity. Nor Galois representations. These are all new terms to me. I am continuing to learn... |
- "Since the time of ... Descartes, mathematicians have realized that the degree of a polynomial is a good indication of how complicated it is." [p. 67]
- This chapter focuses on quadratic equations (i.e. of degree 2) and on only one aspect of them - quadratic reciprocity.
Consider the quadratic equation  (or equivalently, (or equivalently,  ) and let a = 1. ) and let a = 1.
Then S(Z) = {1, -1}
Note the notation. S(Z) may be read as "the solution set over the field Z of integers for the equation  and let a = 1, is {1, -1}. and let a = 1, is {1, -1}. |
Now suppose a = -1.
Then S(Z) is the empty set, so is S(Q) and S(R). But S(C) is {i, -i}.
The real fun, and interest, begins when we consider the solution sets using various groups with a prime generator. (i.e.  ). ).
|
|
Mathematics 14
October 25
|
|
Mathematics Chronology |
8:00 am
I have read chapter 6 Equations and Varieties this morning.
There are both some genuinely new concepts for me as well as some notational conventions. This chapter may require a few re-readings before I move on.
I am reminded of a quote of Richard Feynman's where we suggested that when you read something you don't understand, go back to the beginning of the book and start over. It is good advice. The difficulty is due to a lack of understanding of something that has gone on before, but which, since you didn't 'get it" the first time, you also don't realize that you have missed it.
The first chapter is about Representations. Yet this is not a term that I can now use with comfort. Back to chapter 1.
The two major ideas so far are those of a group and those of a field.
A group is a set of elements and a binary operation (often called a composition) that describes how to obtain an element given two other elements. The set is closed under this operation (i.e. given any two elements in the set and the operation, one always obtains another element in the set). There is an identity element (usually represented by the letter e) such that for any element in the group, xe = ex = x. Every element has an inverse (i.e. xy = yx = e). Finally, the associative law holds for the operation (i.e. for any three elements, (xy)z = x(yz) ).
A field is a special type of group that has a second binary operation (the two operations are usually called addition and multiplication) where element has a multiplicative inverse. One example of a field is the set of integers 0, 1, 2, ... (p - 1) where p is a prime integer and the two operations of addition and multiplication modulo p.
Here is a concept map of the major ideas described in the first 5 chapters.
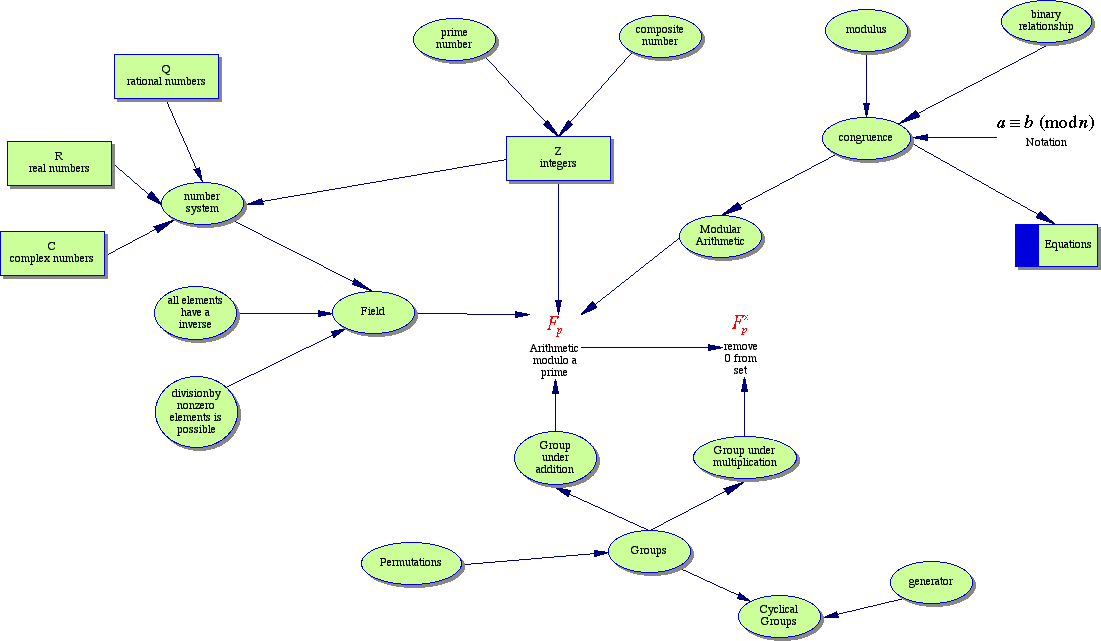
Now to make some notes for chapter 6. Making these notes also acts as a form of consolidation. |
Fearless Symmetry Chapter 6 Equations and Varieties [p. 49 - 66]
- "We now come fact to face with the motivating problem of this book: equations and how to solve them." [p. 49]
- "Although ... we are primarily interested in integral or fractional solutions of systems of polynomial equations with integral coefficients ..., it will be helpful to consider also
- equations and their solutions in general, and
- solutions to equations involving number systems other than the integers." [p. 49]
- "In this chapter we broach the question: 'What are interesting structural properties of sets of solutions.' " [p. 49]
- "Many different systems of equations can define the same variety S." [p. 58]
- "Are there general methods to solve systems of polynomial equations? No." [p. 63]
- "S(A) is not just a set; it is the basis for defining a representation of a certain group, called the Galois group." [p. 66]
- Z-varieties ... leads us to the central subject of this book: Galois groups and their representations
Notations:
- Z, Q, R, C,

- S(A)
Terms
- rational number
- irrational number
- Z-equation
- variety
- roots of f(x)
- Galois groups
- elliptical curves
There were a number of new concepts and terms in this chapter: Z-equation, variety, Galois group and elliptical curves are all totally new to me. This is getting interesting!
Chapter 7 Quadratic Reciprocity [p. 67 - 83] begins by examining some special Z-equation systems and their associated varieties. |
2:30 PM I have just finished reading chapters 3 & 4 of "The Equation That Couldn't be Solved". This provides a superb historical description of the state of mathematics in the 17th century and the relationship between solving equations and that of group theory. It is a nice supplement to "Fearless Symmetry" as it gives a richer sense of the setting within which the mathematical developments occurred, although it does not give much of the actual mathematics. (At least not yet.) |
|
|
Mathematics 13
October 23
|
|
Mathematics Chronology |
6:20 am
The first step for each session should be a review of the previous session's notes. The first few paragraphs of my previous session deserve repeating.
The two major ideas so far are those of a group and those of a field.
A group is a set of elements and a binary operation (often called a composition) that describes how to obtain an element given two other elements. The set is closed under this operation (i.e. given any two elements in the set and the operation, one always obtains another element in the set). There is an identity element (usually represented by the letter e) such that for any element in the group, xe = ex = x. Every element has an inverse (i.e. xy = yx = e). Finally, the associative law holds for the operation (i.e. for any three elements, (xy)z = x(yz) ).
A field is a special type of group that has a second binary operation (the two operations are usually called addition and multiplication) where element has a multiplicative inverse. One example of a field is the set of integers 0, 1, 2, ... (p - 1) where p is a prime integer and the two operations of addition and multiplication modulo p.
Now to make some notes for chapter 5. Making these notes also acts as a form of review. |
Fearless Symmetry Chapter 5 Complex Numbers [p. 42 - 48]
- "Complex numbers are an extension of the real numbers useful for solving equations." [p. 42]
- "The set of complex numbers is another example of a field." [p. 42]
- "It [complex numbers] is handy because every polynomial in one variable with integer coefficients can be factored into linear factors if we use complex numbers. Equivalently, every such polynomial has a complex root. This gives us a standard place to keep track of the solutions to polynomial equations." [p. 42]
- "We also introduce an important subset of the complex numbers, namely, the set of all 'algebraic numbers' - those numbers that are the roots of polynomial equations with integer coefficients. This set is also a field, and will be important when we study the structure of solutions of polynomial equations." [p. 42]
Notations:
Terms
- algebraic numbers
- real number
- complex number
- real part
- imaginary part
- complex conjugate
- theorem
- lemma
- corollary
- algebraically closed
Theorems
5.2 Let f(x) be a polynomial whose coefficients are any complex numbers. (For example, f(x0 might have integer coefficients.) Then the equation f(x) = 0 has solutions in C.
The only real new concept for me is that of an algebraic number. Although I must admit that the term complex conjugate is one that I had forgotten. However the entire emphasis of this book (i.e. solving polynomial equations) is new to me.
I was not aware that complex numbers were useful in understanding polynomial equations. |
- "Multiplication by i rotates the complex plane by 90° counterclockwise as we look down upon it, while -i rotates it the same amount clockwise." [p. 43]
I have just learned how to type the symbol for degrees ( ° ). It is the keystroke alt-shift-8. I googled "symbol for degrees" to discover this. Simple, when you know how.
There is reference to the book "Imagining Numbers" by Mazur, which I happen to have. I must have another look at this book! |
- Definition: A real number is any number that can be expressed as a decimal. [p. 43]
- The set of all real numbers is usually denoted by the symbol R. [p. 43]
- If one tries to solve a cubic equation using a formula like the one for solving quadratic equations, then one unavoidably encounters the square root of a negative number. This was the motivating force behind the creation of complex numbers. [p. 44]
- Definition: A complex number is a number of the form a + bi, where a and b are real numbers.
- Addition and subtraction of complex numbers is simple: just add (or subtract) the real and imaginary parts separately. That is:
(a + bi) + (c + di) = (a + c) + (b + d)i
- Multiplication of complex numbers is defined as follows: (a + bi)(c + di) = ac + adi + bci + bdii = (ac - bd) + (ad + bc)i
- Division by complex numbers is defined as multiplication by the reciprocal. The reciprocal of a complex number turns out to be a fairly complex expression (no pun):

This was a basic chapter. But it whets the appetite for the next chapter where this book begins to take off: the solutions of equations.
Now to begin reading chapter 6 Equations and Varieties [p. 49 - 66] |
|
|
Mathematics 12
October 19
|
|
Mathematics Chronology |
6:40 am
The first step for each session should be a review of the previous session's notes.
The two major ideas so far are those of a group and those of a field.
A group is a set of elements and a binary operation (often called a composition) that describes how to obtain an element given two other elements. The set is closed under this operation (i.e. given any two elements in the set and the operation, one always obtains another element in the set). There is an identity element (usually represented by the letter e) such that for any element in the group, xe = ex = x. Every element has an inverse (i.e. xy = yx = e). Finally, the associative law holds for the operation (i.e. for any three elements, (xy)z = x(yz) ).
A field is a special type of group that has a second binary operation (the two operations are usually called addition and multiplication) where element has a multiplicative inverse. One example of a field is the set of integers 0, 1, 2, ... (p - 1) where p is a prime integer and the two operations of addition and multiplication modulo p
I want to play with this a bit by creating the addition and multiplication tables for  , ,  , ,  and and  . Of particular interest are the tables for . Of particular interest are the tables for  as the generator for this set is not a prime number. as the generator for this set is not a prime number.
 + |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
|
 * |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
 + |
0 |
1 |
2 |
0 |
0 |
1 |
2 |
1 |
1 |
2 |
0 |
2 |
2 |
0 |
1 |
|
|
 * |
0 |
1 |
2 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
2 |
0 |
2 |
1 |
|
 + |
0 |
1 |
2 |
3 |
0 |
0 |
1 |
2 |
3 |
1 |
1 |
2 |
3 |
0 |
2 |
2 |
3 |
0 |
1 |
3 |
3 |
0 |
1 |
2 |
|
|
 * |
0 |
1 |
2 |
3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
3 |
2 |
0 |
2 |
0 |
2 |
3 |
0 |
3 |
2 |
1 |
|
Multiplication falls apart in the case where the modulus is a composite number. The last table does not satisfy the criteria for a field. |
Fearless Symmetry Chapter 4 Modular Arithmetic [p. 31 - 41]
- "... modular arithmetic ... is our way of dealing with dvisibility of numbers and remainders." [p. 39]
- "... modular arithmetic gives us not one but two groups for each prime p." [p. 39]
- "
 is a group under addition. The neutral element is 0. The inverse of any number a (mod p) is just p - a (mod p)." [p. 39] is a group under addition. The neutral element is 0. The inverse of any number a (mod p) is just p - a (mod p)." [p. 39]
- "If we throw 0 away from
 , we get a new set, with only p - 1 elements, called , we get a new set, with only p - 1 elements, called  , pronounced 'eff-pea-cross'. It is a group under multiplication." [p. 39] , pronounced 'eff-pea-cross'. It is a group under multiplication." [p. 39]
- "We can use congruences to prove that some equations have no integral solutions." [p. 41]
Example: There are no integers x and y with the property  . .
Suppose there were two such integers, x and y.
Since  , then , then  since if since if  , then , then  modulo any number we like. modulo any number we like.
Consider the squares: they are 0, 1, 4, 9, 16, 25, 36, 49, ... . Modulo 4 they are 0, 1, 0, 1, 0, 1, 0, 1, ... So  is either 0 or 1 modulo 4. The same is true for is either 0 or 1 modulo 4. The same is true for  . Therefore their sum must be either 0, 1, or 2. Now consider 11. It is 3 (mod 4). Therefore it cannot be the sum of two squares. . Therefore their sum must be either 0, 1, or 2. Now consider 11. It is 3 (mod 4). Therefore it cannot be the sum of two squares.
This is so neat!
Using MathType within OS X is working quite well for the mathematical notation.
Now to move away from the screen and read chapter 5 Complex Numbers. |
|
|
Mathematics 11
October 18
|
|
Mathematics Chronology |
6:00 am
It has been almost a week since I made any mathematical notes. As I noted in my last session, there are two issues: understanding what one is doing, and learning how to represent this action using a specialized notation. Chapter 4 of Fearless Symmetry has more mathematics embedded in it than the previous chapters. It is easy to become overwhelmed by it.
The first step is to identify the new terms and concepts. The basic idea of modular arithmetic is one that I am familiar with. However some of the terms and even some of the notation is genuinely new to me. Great. |
Fearless Symmetry Chapter 4 Modular Arithmetic [p. 31 - 41]
Notations:
Key People:
- Gauss
- German
- considered one of the greatest mathematicians of all time
- originated the modern notation for modular arithmetic
- Dirichlet
- German
- proved an important theorem on prime numbers, which now has his name attached to it. "An arithmetic progression contains an infinite number of primes if there is no gcd > 1 for all the numbers in the progression."
Terms
- binary relation
- congruence
- congruent modulo n
- modulus
- integer
- prime number
- composite number
- arithmetic progression
- field
- characteristic
- Euclidean algorithm
- cyclic group
- generator of a group
A good beginning.
The % notation is new to me. Apparently it is preferred by computer scientists. I wonder why. The notation means "the remainder when a is divided by n".
A slightly more complex idea is embodied in the notation developed by Gauss. a  b (mod n) means that both a and b have the same remainder when divided by n. The two numbers are said to be congruent modulo n. b (mod n) means that both a and b have the same remainder when divided by n. The two numbers are said to be congruent modulo n.
Integers, prime numbers, composite numbers and arithmetic progressions are basic ideas that I have known since early undergraduate days. (I cannot recall if we met prime numbers in high school. They should be introduced in elementary school as they are one of the intriguing ideas in mathematics and it is good to let children realize that mathematics can be intriguing. The book by Conway and Guy called The Book of Numbers is another resource that is full of interesting ideas about numbers.
The mathematical concept of a field is one that I recall taking in a course on Modern Algebra, but I cannot recall anything about it. The terms characteristic, Euclidean algorithm, cyclic group and generator of a group are all new to me. It is time to engage in some new Learning. |
First, for review, here are my earlier notes about groups:
- "The definition of a group is the most common way mathematicians have of formalizing the concept of symmetry. " [p. 13]
- "A group is a set along with a rule that tells how to combine any two elements in the set to get another element in the set." [p. 14]
- "We usually use the word composition to describe the act of combining two elements of the group to get a third." [p. 14]
- "The key point about a group is the combination of any two elements to get a third." [p. 15]
- "DEFINITION: A group G is a set with a composition defined on pairs of elements, as long as three axioms hold true:
1. There is a neutral element e in G, so that x o e = e o x = x no matter what element of the group is substituted for x.
2. For any element x of G, there is some element y in G so that x o y = y o x = e (y is called the inverse of x)
3. For any three elements x, y, and z in G, we have (x o y) o z = x o (y o z). (this is called the associative law)." [p. 17]
- "DEFINITION: If G is a group, the group law is the rule that tells how to combine two elements in the group to get a third. We will usually write this combination as x o y, but occasionally as x + y or even xy." [p. 18]
Now, to go on ...
- "DEFINITION: A field is a number system where we can divide by anything nonzero." [p. 36]
I find the above definition to be unhelpful. It fails (for me) to conjure up any idea or mental image of what we are talking about.
Here is the wikipedia definition of a field: http://en.wikipedia.org/wiki/Field_(mathematics).
I then returned to "Fearless Symmetry" and tried to type in a sentence involving a subscript. Here is the result:
 is defined as the set {0, 1, 2, ... , p-1} with addition and multiplication defined as follows: If x, y, and z are in is defined as the set {0, 1, 2, ... , p-1} with addition and multiplication defined as follows: If x, y, and z are in  , x + y = z in , x + y = z in  exactly when x + y ∫ z (mod p) and xy = z in exactly when x + y ∫ z (mod p) and xy = z in  exactly when xy ∫ z (mod p). exactly when xy ∫ z (mod p).
Basically, this is the pits. There must be a better way. |
2:00 PM
I googled "mathematics notation Dreamweaver" and found the following web site:
The website mentions MathML (Math Markup Language) that is a new standard for creating mathematical notation within an XML environment. MathType (which I have for Windows) permits one to create web pages that use MathML or to embed a mathematics expression created in MathType (which is very easy) into a web page using MathML created in Dreamweaver. This is exactly what I want to do.
I have downloaded MathType for the Macintosh (OS X) but am having difficulty getting the embedded expression to display properly using Firefox (my web browser). I will play around a bit and see if I can get this working. At present I have a 30-day free trial, so I have time to determine if this will resolve my difficulties.
Here is an example: 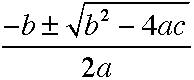
This works just fine. All I am doing is creating an expression in MathType and then saving the expression as a gif file. Nothing technical about this. Let's try my previous example.
 is defined as the set {0, 1, 2, ..., p - 1} with addition and multiplication defined as follows: is defined as the set {0, 1, 2, ..., p - 1} with addition and multiplication defined as follows:
if x, y, and z are in  , ,
x + y = z in  exactly when x + y exactly when x + y  z (mod p) and z (mod p) and
xy = z in  exactly when xy exactly when xy  z (mod p). z (mod p).
|
|
|
Mathematics 10
October 12
|
|
Mathematics Chronology |
7:00 am
I want to continue with "Fearless Symmetry" this morning. I completed the exercise on page 28 last evening. There are very few exercises in this book (it is not a textbook but a book for the individual interested in the ideas of symmetry and how they might be explored using ideas such a groups. Conceptually I felt I understood what I was trying to do with the permutation groups. And I understand the idea of a cycle.
But the challenge is the notation, both written and on the screen. I am beginning to think that it may make more sense to use paper and pen and then scan the result into these notes. |

There are two issues here. One is understanding what one is doing (i.e. first applying a sequence of functions to a set of elements that results in a permutation of these elements). Second is Learning how to represent this action using a notation that is used by mathematicians.
Here is a quote from the book that caught my attention:
"Many people believe that all of mathematics has already been discovered and codified. Mathematicians (they think) do nothing except rearrange the material in different ways for different types of students. This seems to be the result of the cut-and-dried method of teaching mathematics in many high schools and universities. The facts are laid out in the cleanest possible logical order. Little attempt is made to show how someone once had to invent it all, at first in a confused way, and that only later was it possible to give it this neat form. Many textbooks make no effort to tell about directions that are still to be explored, conjectures that are unproven, nor, of course, of ideas that are yet to be formulated.
Project yourself back in time to 1000 BC. Very little mathematics was known then. It all lay in the future to be discovered, debated, arranged, and improved. The situation today is nearly the same!" [p. 29]
8:00 am
|
|
Mathematics 09
October 11
|
|
Mathematics Chronology |
8:30 am
I have had a quick look at most of the mathematics books on my shelves near my computer. It was relatively easy to place the titles into a table in my Project Mathematics web page where I monitor my progress in learning mathematics. However that page is more a place where I keep track of what I have done than a map for what I should be doing in the future.
| Calculus |
|
| |
Calculus (1998) Roland Larson, Robert Hostetler & Bruce Edwards |
| |
Calculus (1994) Michael Spivak |
| |
What is Mathematics? (1996) Richard Courant & Herbert Robbins |
| |
Calculus: An Intuitive and Physical Approach (1977) Morris Kline |
| |
The Calculus Tutoring Book (1986) Carol Ash & Robert B. Ash |
All five book take a different approach to the topic.
The Larson book is the most "modern" in terms of comprehensiveness and use of graphics and imagery. It is also a traditional approach with a large number of problems that provide a high amount of drill and repetition in order for the skill of being able to "do" various types of problems to become automatic. It makes extensive use of technology to obtain graphs of complex situations.
The Spivak book is much more theoretical and abstract with an emphasis on the ideas rather than the skill of applying different algorithms to different situations. One noticeable feature of this book is the large preliminary treatment of ideas that are necessary before discussing the concepts of differentiation and integration. The first 150 pages discuss the nature of numbers, functions , graphs, limits and continuity. There is a lot of basic mathematics here, but treated at a very sophisticated level.
The Ash book is more like an abbeviated Larson book, much less sophisticated from a publishing perspective. The emphasis is not on the formalism of the topic but the general ideas and makes extensive use of hand-drawn sketches.
Kline takes a number of practical problems as the starting point for a discussion of the ideas of calculus. Courant & Robbins describe mathematics in terms of its basic ideas and procedures.
Overall strategy: I will try to read and do the exercises from both the Larson and the Spivak books in parallel. That is, I will cover the same topic in both books before moving on. The Larson book has an initial chapter on graphs and functions followed by a chapter on limits and continuity. Spivak begins with a chapter on numbers and then has separate chapters on functions, graphs, limits and continuity. For each chapter I will create a concept map (using Inspiration) as well as a mind map (using Mindmanager). I will then try to combine these two maps into a diagram that is a synthesis of both images.
Technology continues to be problematic. Most of my mathematics software is specific to windows operating systems whereas I am now using a Mac for my core web authoring (using Dreamweaver). I need to get my windows version on the Mac up-dated for Word so I can use the notation. I also want to install Mathematica on this machine. There is nothing for it but to see what happens when I try this. |
9:20 am Begin installing MathType for windows. That was easy. It was already there!
9:35 am Now to see if I can get Mathematica installed. This has turned out to be an adventure. After I installed the software, it asked for my password. Fortunately I had this written down, but when I tried it, it said it was invalid. After trying my license number, my MathID, and my password, and not having any success, I tried registering it on the web. This appeared to work but it was cumbersome as I was switching back and forth between operating systems and trying to keep track of what was going on. I finally realized that Mathematica had allocated a new MathID to my installation on the Mac and the password was only valid for the MathID that had been assigned for the PC. I went back to the web site and managed to get a new password but it is only valid for 4 days. I then needed to print out a form and fax it to Wolfram. I took it into the university only to find that the key person is away this week. Hopefully this will all resolve itself, but it is annoying (and time consuming).
2:20 PM
In addition to the books, I want to use both MathType (for formatting mathematical expressions for my notes) and Mathematica (to explore more complex expressions quickly).
I have one good book for Mathematica:
| Mathematica |
|
| |
Mathematical Navigator (2004) Heikki Ruskeepaa |
Here is my list of books related to Number Theory:
| Number Theory |
Fundamentals of Number Theory (1977) William J. LeVeque |
| |
Prime Numbers (2005) David Wells |
| |
Dr. Riemann's Zeros (2002) Karl Sabbagh |
| |
Prime Obsession (2003) John Derbyshire |
| |
Stalking the Riemann Hypothesis (2005) Dan Rockmore |
| |
The Music of the Primes (2003) Marcus du Sautoy |
| |
Numbers (1983) Graham Flegg |
| |
The Art of the Infinite (2003) Robert Kaplan & Ellen Kaplan |
| |
The Book of Numbers (1996) John H. Conway & Richard K. Guy |
| |
Mathematical Mysteries. The Beauty and Magic of Numbers (1996) Calvin C. Clawson |
| |
Wonders of Numbers (2001) Clifford A. Pickover |
I am not yet sure how I want to proceed with this topic. I will conduct a few searches on the Web for "number theory courses" and "number theory textbooks" and see if I can see something that catches my eye.
I have definitely found one book that looks interesting: Elementary Number Theory in Nine Chapters (2005) by James J. Tattersall.
Under Special Topics, I have two books:
| Special Topics |
|
| |
|
| Symmetry & Group Theory |
Fearless Symmetry (2006) Avner Ash & Robert Gross |
| |
The Equation that Couldn't Be Solved (2005) Mario Livio |
I am reading and making notes for the first book and have just realized that the second book also covers much of the same material.
Now for a few priorities. My first priority at the moment is the Fearless Symmetry book. My second priority will be a return to calculus. More than two priorities are no priorities. |
|
|
Mathematics 08
October 09
|
|
Mathematics Chronology |
6:40 am
Fearless Symmetry. Chapter 2 Groups [p. 13 - 20]
- "The definition of a group is the most common way mathematicians have of formalizing the concept of symmetry. " [p. 13]
- "A group is a set along with a rule that tells how to combine any two elements in the set to get another element in the set." [p. 14]
- "We usually use the word composition to describe the act of combining two elements of the group to get a third." [p. 14]
- "The key point about a group is the combination of any two elements to get a third." [p. 15]
- "DEFINITION: A group G is a set with a composition defined on pairs of elements, as long as three axioms hold true:
1. There is a neutral element e in G, so that x o e = e o x = x no matter what element of the group is substituted for x.
2. For any element x of G, there is some element y in G so that x o y = y o x = e (y is called the inverse of x)
3. For any three elements x, y, and z in G, we have (x o y) o z = x o (y o z). (this is called the associative law)." [p. 17]
- "DEFINITION: If G is a group, the group law is the rule that tells how to combine two elements in the group to get a third. We will usually write this combination as x o y, but occasionally as x + y or even xy." [p. 18]
- Groups that have infinitesimal generators are called continuous groups These are also known as Lie (pronounced lee) groups. Groups that have no smooth path from one element to another are called discrete groups.
- Continuous groups
- rotations of a sphere inside a cube with composition being successive rotations
- rigid motions in space
- rotations of a circle
- set of real numbers with composition given by ordinary addition.
- Discrete groups
- set of all integers with addition
- permutation group.
The idea of a group is an easy one. What is not quite so obvious is why this is a "good" idea. The connection between the concept of a group and that of symmetry is not yet obvious either.
The rest of this chapter is simply that of a few terms (group, composition, neutral element, inverse element) as well as notation (how to express the composition).
It is worth noting that there are many different "types" of group, each with different properties. The Lie groups are particularly interesting as they describe continuous compositions and are analogous to continuous functions in calculus.
The next chapter is about permutation groups, a special form of discrete group. |
7:20 am
8:05 am
I have read chapter 3 Permutations [p. 21 - 30].
As with the previous chapter there is only one fundamental idea in the chapter, that of a permutation group. However there is some fairly complicated notation associated with this idea. |
Fearless Symmetry. Chapter 3 Permutations [p. 21 - 30]
- "Permutation groups ... are essential for our later definition of Galois groups. Galois groups are permutation groups of a certain kind: they permute roots of polynomials." [p. 21]
- A permutation is a particular ordering of the elements of a given discrete set. A permutation group is the set of all possible orderings (i.e. each element of the group is a particular ordering).
- "The group of permutations of A is the set of functions from A to itself that are one-to-one correspondences. Composition of permutations are the composition of functions." [p. 25]
- "The neutral permutation e in a group of permutations of A is called the identity permutation." [p. 25]
- The permutations of a given set A are always a group, using composition to combine pairs of elements. We use the symbol sigma sub A to denote this group.
| I am unable to easily type the symbol for sigma sub A using Dreamweaver. I think I will have to install MathType into the Windows version of Word and then use Parallels to switch between operating systems and use Grab to capture the image and paste it into this file. |
- "One of the niftiest elementary things about a permutation is called its cycle decomposition." [p. 26]
|
|
Mathematics 07
October 08
|
|
Mathematics Chronology |
10:15 am
I have just created a concept map for the first two chapters of "Fearless Symmetry". This is one of the clearest introductions to group theory that I can recall. |

I still want to make a few additional notes on chapter 2 where I capture some important sentences and ideas, but it is time for a break and a return to reality. |
Chapter 2 Groups [p. 13 - 20]
10:30 am
|
|
Mathematics 06
October 07
|
|
Mathematics Chronology |
5:15 am
I began reading "Fearless Symmetry" yesterday evening. The book looks to be interesting, accessible, and contain a lot of mathematics that is genuinely new to me. Great!
Equally challenging is to come up with a format for making notes about this book. I lean toward some form of diagram or schematic image as a supplement to more verbal notes such as direct quotes and summary statements. The whole point of the notes is to make explicit to myself my understanding of what is being said. I want to play a bit with both Inspiration and MindManager software. |
The subtitle of the book is "Exposing the Hidden Patterns of Numbers".
Both the title and the subtitle attracted me to the book. I have always been interested in the topic of symmetry and the idea of looking for the hidden patterns of numbers was intriguing. |
Foreward [p. xv - xix] (by Barry Mazur)
- "Fearless Symmetry begins where few math books do, with an enlightening discussion of what it means for one 'thing' to represent another 'thing'. This action - deeming A a 'representation' of B - underlies much mathematics. ... What an extraordinary concept representation is and always has been. In Leibniz's essay On the Universal Science: Characteristic where he sketched his scheme for a universal language that would reduce ideas 'to a kind of alphabet of human thought,' Leibniz claimed his characters (i.e. the ciphers in his universal language) to be manipulable representations of ideas.
All that follows rationally from what is given could be found by a kind of calculus, just as arithmetical or geometrical problems are solved.
" [p. xvi]
This is not the first time I have seen reference to Leibniz's idea of a universal language for manipulating ideas, but I think it has been over 20 years. I do recall encountering the idea while I was at Queen's University.
A variation on this theme of representation might be that of diagrams. I think of Richard Feynman's diagrams for representing sub-atomic interactions as an example. I want to play with this using both Inspiration and MindManager software. The driving force is that of how to represent ideas and to show how they interact with one another. In Learning mathematics one should have as clear an idea (or complex of ideas) as one can about exactly what it is that one is doing. Unfortunately this has degenerated into the algebra of symbolic logic and proof and in the process the idea itself has become lost. This is particularly true in the case of students who are being introduced to new ideas and procedures in mathematics courses.
The issue of representation is fundamental, not only to mathematics, but also to psychology. Jerome Bruner identified this in his writings of the 1960's when he distinguished between iconic, symbolic and enactive representations. |
Preface [p. xxi - xxv]
- This book is a popular exposition of cutting-edge research in one important area of mathematics, number theory." [p. xxi]
Play time.
Let's try to capture a few ideas that seem to be central to this book:
- mathematics
- number theory
- representation
- symmetry
- idea
- concept
How can one represent these ideas?
One approach, an excellent one, is to write a paragraph or two describing what each term "means", perhaps give an example or two, and then mention some of the relationships that exist among the terms. Let's try this.
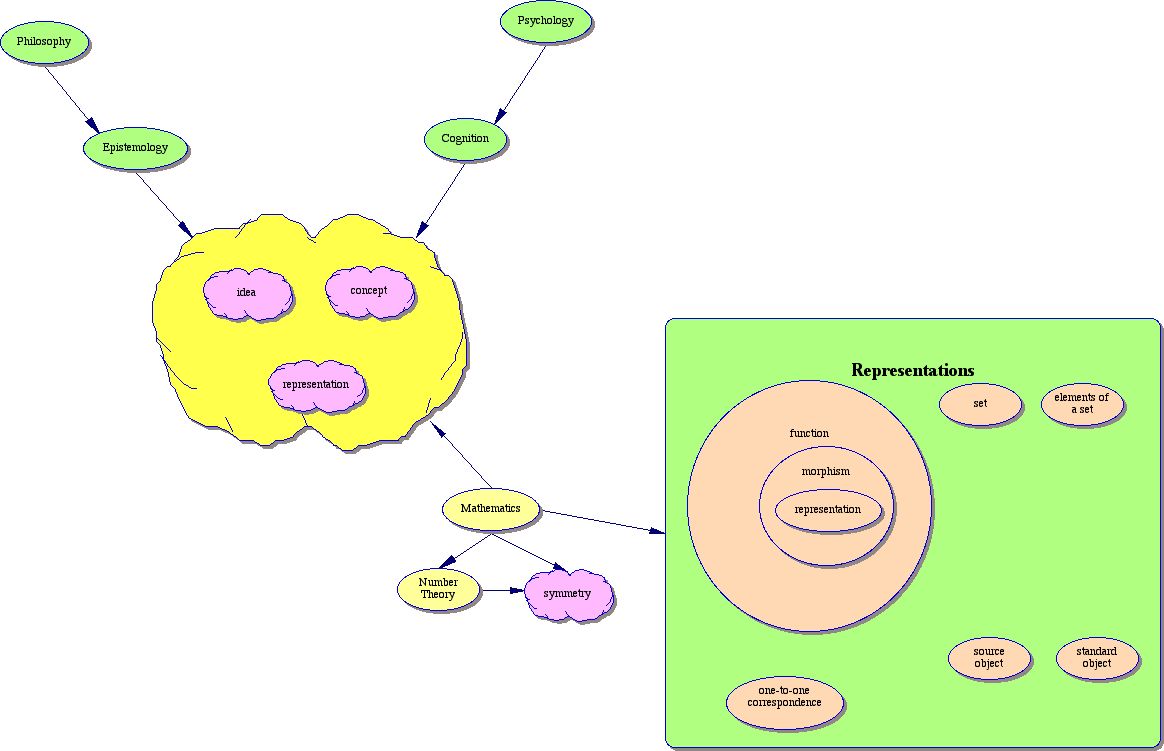
Mathematics is a branch of knowledge that is primarily about numbers and quantities and the logic of the relationships among them. There are many topics within mathematics (hundreds) although it is often difficult to make clear demarcations between these topics. One of the popular topics is that of number theory which is primarily about relationships and patterns among the integers. When one begins to discuss patterns, one then encounters the idea of symmetry which refers to a particular type of pattern. There are many different kinds of symmetry. All of this may be thought of as being embedded within the meta-branch of knowledge commonly referred to as psychology, although a good claim can be made that psychology is embedded within philosophy - particularly that branch of philosophy called epistemology.
Here is one possible representation of the ideas we have encountered so far.
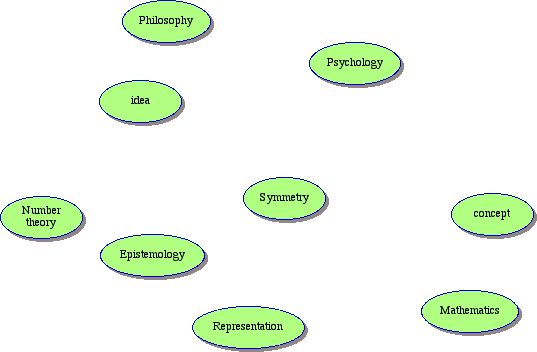
At the moment it is an amorphous jumble of ovals. For many Learners this may be a fairly good representation of their understanding at this point. There is much to commend this representation. It provides a visual image of the ideas, as well as a linguistic one. There is a fluidity implicit in the diagram. The various ovals could be placed in different locations. One may wish to try using different shapes or colors or sizes to, in some sense, improve the representation.
Here is one such image:

This latter diagram emphasizes that there are four ideas (representated by the pink "clouds", and 6 categories represented by the ovals. The large yellow cloud shows that the ideas of idea, concept and representation are important to philosophy, psychology and mathematics.
Now lets have a look at the MindManager representation.
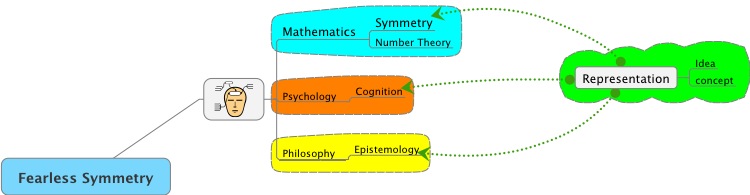
Both images show that the core ideas of representation, idea and concept are fundamental to mathematics, psychology and philosophy.
|
Chapter 1 Representations [p. 3 - 12]
- "... the basic concept of representation ... is the key concept underlying the number-theoretic methods of Galois representations that are our goal." [p. 3]
- "Say B represents A. We have three terms that stand together in some kind of relationship: A, B, and the fact that B represents A. We can call this fact X. ... Now what would be a good picture of A, B, and X?" [p. 4]
Lovely! What constitutes a "good picture"? Are the two diagrams that I produced using Inspiration and MindManager good pictures?
Frustration of a sort. Neither Inspiration nor MindManager are able to produce the simple images of a box with an arrow showing the existence of a relation between A and B.
Here is one such diagram, drawn using EazyDraw.

But this is much more trouble than it is worth. Technology sometimes falls far short of pencil and paper! The best I can do with the keyboard is x: A -> B |
- "What are representations used for? They explain one thing by means of another. The object that we want to understand is the 'thing': the thing-in-itself, the source. The object that we know quite a bit about already, to which we compare the source via a representation, we call the standard object. ... The target, the object at the head of the arrow, is the piece of the picture that we understand better. We will derive information about the source by using properties of both the arrow and the target." [p. 5]
- "DEFINITION: A set is a collection of things, which are called the elements of the set." [p. 6]
- "DEFINITION: A one-to-one correspondence from a set A to a set B is a rule that associates to each element in A exactly one element in B, in such a way that each element in B gets used exactly once, and for exactly one element in A." [p. 6]
- Counting viewed as a representation: Suppose A is a collection of things and B is the set of counting words.
In my own words: A representation is a pair of sets and a rule that describes the relation between the elements of each set. |
- "DEFINITION: A function from a set A to a set B is a rule that assigns to each element of A an element of B." [p. 9]
- "DEFINITION: A morphism is a function from A to B that captures at least part of the essential nature of the set A in its image in B." [p. 9]
- "DEFINITION: A representation is a morphism from the source object to a standard target object." [p. 10]
- "If A represents B, we have three things: two objects, A and B, which from now on will be sets, and the relation between them, which from now on will be a morphism. When A and B have some additional 'structure' - e.g. they are finite sets, or ordered sets - and we restrict the possible morphisms from A to B to have something to do with that structure - e.g. morphisms must be one-to-one correspondences, or order-preserving functions - then the existence of a representation from A to B gives us some information about A in terms of the standard object B." [p. 11]
- "In this book we will explore some very explicit examples of representations. The things we consider are always mathematical objects such as sets, groups, matrices and functions between them." [p. 11]
Let's go back to the first diagrams I created for this chapter.
The ideas are very simple and straightforward, although the language and new terminology may appear at first sight to be convoluted and complex. A representation is a special kind of morphism which is a special kind of function. In other words, a representation is a rule that describes the relationship between two objects, usually called the source object and the standard object.
|
9:30 am
|
|